Теорема Тейлора о разложении голоморфной функции в степенной ряд. Следствия: существование у голоморфной функции производных всех порядков, интегральная формула для производных

Теорема Пусть f(z) – голоморфная, z∈G, R.В круге K_R={z:|z-z₀|<R}, функция f(z) представляется в виде степенного ряда:

Доказательство: z∈K_ρ, рассмотри коцентрический круг  радиуса  (0< <R), содержащий z.

При фиксированном z последний ряд равномерно сходится на Г_ρ (ξ∈Г_ρ).

так что можно воспользоваться мажорантным признаком Вейерштрассе равномерной сходимости ряда. В (2) законно почленное интегрирование ряда (3):

Следствие 1 Каждая функция f(z), голоморфная в области G имеет производную всех порядков в этой области. Следствие 2
Следствие 3

 

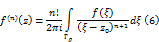
15. Неравенства Коши для коэффициентов степенного ряда и теорема Лиувилля. Основная теорема алгебры.Теорема 1 (неравенства Коши)

Неравенства (3) называются неравенствами Коши.

Доказательство:

Теорема 2 (теорема Лиувилля)

Если функция f(z) голоморфна на всей плоскости C_z, и |f(z)|<M, M>0, то f(z)=const

Доказательство:

Радиус сходимости разложения (1) равен бесконечности, т.е. неравенства (3) имеют место для ⱯR>0. Отсюда получим: a_n=0, при (n=1,2,…). И стало быть f(z)=a₀=const

Теорема 3 (основная теорема алгебры)

Всякий многочлен p(z)=c₀+c₁z+…+c_nzⁿ (n≥0, c_n≠0) имеет хотя бы один нуль.

Доказательство:

По т. Лиувилля f(z)=const=0, что противоречит определению этой функции.

ч.т.д.

 

 

Теорема о существовании первообразной у голоморфной функции. Формула Ньютона-Лейбница.

Теорема 1

Если функция f(z) голоморфна в односвязной области G, то значения интеграла

и конечного пути интегрирования.

Теорема 2

Пусть f(z) – функция, неприрывная в односвязной области G, для которой итегралы вдоль любых спрямляемых кривых, принадлежащих области, зависят только от начальных и конечных точек

F’(z)=f(z)

Определение

Назовем функцию Ф(z) голоморфную в области G первообразной для функции f(z), если Ф'(z)=f(z).

Теорема 3

Любая первообразная Ф(z) от голоморфной в области G функции f(z) выражается формулой:

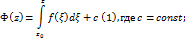
Доказательство:

 

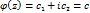
ч.т.д.

 

Полагая в (1) z=z₀, получим: Ф(z₀)=с, поэтому из (1) следует формула Ньютона-Лейбница:

 

 

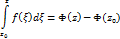
Гармонические функции. Восстановление голоморфной функции по её действительной части. Сопряжённые гармонические функции. Бесконечная дифференцируемость гармонических функций.

Определение 1

Однозначная в области Gдействительная функция u(x,y) действительных переменных

x, y ∈ R, обладающаянеприрывными частными производными 2-ого порядка и

Теорема 1

Действительная и мнимая части голоморфной в некоторой области функции обладают дифф. Частными производными всех порядков и являются функциями гармоническими в той же области.

Теорема 2

По ф-ии u(x,y), гармонической в односвязной области G, можно найти такую аналитическую функцию f(z), что Re f(z)=u(x,y). Эта функция определена с точностью до постоянного, чисто

где (x₀,y₀) –фиксированная точка в области G.

Определение 2

Гармонические функции u(x,y), v(x,y) такие, что функция f(z)=u+iv является голоморфной функцией переменного z=x+iy называются взаимно-сопряженными.

 

18. Теорема Мореры.

Теорема: Если ф-ия непрер-на в односвязной обл. G и , взятый по контуру , равен нулю, то f(z) голоморфна в G.

Док-во:  вытекает обращение в 0 ин-ла вдоль  замкн. спрямл. кривой, леж. в G. Это равн-но тому, что  зависит только от нач. и кон. т. Г.

Для  кривой Г с G (т.1п.9)

Пот т.2п.9  (z0,z  явл. голоморфной ф-цией в G, причем F’(z)=f(z).

Отсюда в силу диф-ти ф-ии F(z) любое число раз (сл.1п.7) сл. сущ-ие F’’(z)=f’(z), z . Т.о., ф-ия f(z) голоморфна в G.

Теорема 1(п.9): Если ф-ия f(z) голоморфна в односвяз. обл. G, то знач. ин-ла , взятого вдоль спрямл. кривой Г с G, зависит от начал. и конеч. точек пути интегрирования.

 

19. Теоремы Вейерштрасса о последовательностях и рядах равномерно сходящихся голоморфных функций.

Теорема 1: Если каждая ф-я f_n (n  непр-на на спрямл. кривой Г с С_я и посл-ть {f_n} равном. сходся на Г, то

Опред. Говорят, что некот. св-ва имеют место внутри обл.G С_я, если оно выполн. на каждом замкн. огранич. мн-ве, лежащ. в этой обл-ти.

Теорема 2: Если кажд. ф-ия f_n(n 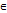N) голоморфна в обл. G с С_z и посл-ть {f_n} равномерно сход. внутри G к f, то f-голоморфна к G и {f_n^(k)} (k  сход. в G к f^(k).

Теорема 3: Если кажд. ф-ия f_n (n  голоморф. в обл. G и ряд  равном. сход-ся внутри G к S(z), то S(z) голоморфна в G и ряд 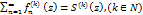 сход-ся в G.

20. Теорема Единственности голоморфной функции.

Теорема: Пусть ф-я f голоморфна в обл. G с С_z и обр. в нуль на беск. множ-ве E точек, имеющих конечную предельную точку в обл. G, тогда f=0.

Док-во: Пусть z₀- предел. точка мн-ва E, z_{0 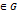,} тогда в силу непрер-ти f имеем f(z₀)=0. По т.Тейлора ф. f можно представить рядом степени z-z₀ в нек. окр. V(z₀, ) т.z₀. Пусть C_m, (m - это первый, отлич. от нуля, коэф. ряда *(z-z₀)^m+…=(z-z₀)^m * , где =С_m+С_m+1(z-z₀)+…(С_m≠0)-голоморф. в окр-ти V функция, ≠0. Поскольку -непрер. в т. z₀, сущ. окр-ть V(z₀, ), в котор. ≠0, тогда в V(z₀, ), ( =min { , }) ф-ия  обращается в нуль в т. z₀, что противоречит опред. т. z₀ как предел. т. множ-ва, на кот. f=0. Т.о., все коэф. разлож-ия ф. f в ряд Тейлора в окр-ти V(z₀, ) равны 0 и f=0 в окр-ти V(z₀, ). Пусть z^*-любая фиксир. т. в обл-ти G. Соединим z₀ и z^*ломанной L с G с конеч. числом звеньев. Пусть d – расст. L до . Рассм-м круг U_s=U(z_s,  () c центром в т. z_s . z₀,z₁,…,z_n выберем на L так, чтобы z_s+1 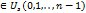, а т. z^* c U_n. Тогда f=0 в каждой из этих окр-ей в U_s, s=0,1,…n. Дей-но, при s=0 утв. уже доказано. Предположим, что f=0 в круге U_s (s≤n-1), центр z_s+1 круга U_s+1 содерж. в U_s, и, сл-но, явл. предел. точкой для бескон. мн-ва, на кот. f=0. Согласно доказанному, сл-т, что f=0 в U_s+1 + в U_n, f(z^*)=0.

Сл-ие: Если ф-ии f и g, голомор. в обл. G, равны на беск. мн-ве. т., имеющ. предел т. G, то f=g в G.