Пусть дано:
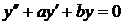 , (1)
, (1)
где  ,
,  – действительные числа. Составим так называемое характеристическое уравнение:
– действительные числа. Составим так называемое характеристическое уравнение:
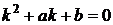 (2)
(2)
и найдем  ,
,  – корни уравнения (2), и пусть
– корни уравнения (2), и пусть  . Рассмотрим две функции:
. Рассмотрим две функции:
 и
и  . (3)
. (3)
Докажем, что  и
и  есть частные решения, образующие фундаментальную систему решений. Подстановка дает:
есть частные решения, образующие фундаментальную систему решений. Подстановка дает:
 и
и  ,
,
 , (4)
, (4)
следовательно, общее решение
 ,
,
где  ,
,  –
–  .
.
Если  и
и  – комплексно сопряженные числа,
– комплексно сопряженные числа,  ,
,  , то (4) дает решение в мнимой форме. Но можно получить и в действительной, если перейти к
, то (4) дает решение в мнимой форме. Но можно получить и в действительной, если перейти к

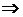 (5)
(5)
 (6)
(6)
– общее решение.
Примеры:
1)  ,
,  ,
,  .
.
2)  ,
,  ,
,  .
.
3)  ,
,  ,
,  .
.
Рассмотрим теперь случай  . В этом случае
. В этом случае  , а
, а  можно получить, используя формулу Остроградского – Лиувилля:
можно получить, используя формулу Остроградского – Лиувилля:
 ,
,
 ,
,
значит,  и
и  – фундаментальная система решений. Общее решение будет
– фундаментальная система решений. Общее решение будет
 . (7)
. (7)
Неоднородные линейные дифференциальные уравнения 2-го порядка с постоянными коэффициентами
Дано:
 , (8)
, (8)
 и
и  – действительные числа, соответствующее однородное уравнение имеет вид:
– действительные числа, соответствующее однородное уравнение имеет вид:
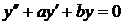 ,
,
характеристическое уравнение будет:
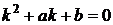 .
.
При известном общем решении однородного дифференциального уравнения частное решение неоднородного находится вариацией постоянных, а затем составляется общее решение (8). Метод вариацмм применим к (8) при  и в этом смысле универсален. Однако, для частных случаев
и в этом смысле универсален. Однако, для частных случаев  чаще применяется метод подбора.
чаще применяется метод подбора.
Общее правило. Если  может быть представлена в виде
может быть представлена в виде
 , (9)
, (9)
где  ,
,  – действительные числа,
– действительные числа, 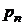 и
и 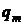 – целые рациональные функции степеней
– целые рациональные функции степеней  и
и  , тогда (8) имеет частное решение вида
, тогда (8) имеет частное решение вида
 . (10)
. (10)
Здесь  – кратность корня
– кратность корня  характеристического уравнения. Если же
характеристического уравнения. Если же  не является корнем, то
не является корнем, то  .
.  ,
,  и
и  – многочлены степени
– многочлены степени  . Коэффициенты
. Коэффициенты  и
и  определяются из тождества после подстановки
определяются из тождества после подстановки  в (8). Далее, как обычно, общее решение есть сумма
в (8). Далее, как обычно, общее решение есть сумма  и
и 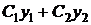 .
.
Если же  не может быть сразу представлена в виде (9), но является суммой таких выражений, то используется теорема о наложении решений.
не может быть сразу представлена в виде (9), но является суммой таких выражений, то используется теорема о наложении решений.
Для обоснования рассмотрим два частных случая  и выведем правила нахождения
и выведем правила нахождения  для каждого случая.
для каждого случая.
Случай 1.
 ,
, 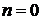 ,
,  –
–  .
.
Этот случай соответствует  .
.  будем искать в виде
будем искать в виде  . Подставим
. Подставим  в (8), получим
в (8), получим
 ,
,
где 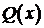 есть:
есть:
1) многочлен  -ной степени, если
-ной степени, если 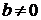 .
.
2) многочлен  -й степени, если
-й степени, если  ,
,  .
.
3) многочлен  -й степени, если
-й степени, если  .
.
В первом случае 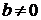 приходим к тождеству
приходим к тождеству
 , (*)
, (*)
из которого можно найти неопределеные коэффициенты  .
.
Во втором случае,  ,
,  , то есть когда
, то есть когда  есть корень характеристического уравнения, тождество (*) невозможно, так как степень
есть корень характеристического уравнения, тождество (*) невозможно, так как степень 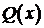 на 1 меньше степени
на 1 меньше степени  . Чтобы их сравнять, надо умножить
. Чтобы их сравнять, надо умножить  на
на  . При этом степень
. При этом степень 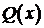 повышается на 1. То есть мы будем искать решение в виде
повышается на 1. То есть мы будем искать решение в виде
 .
.
В третьем случае  умножается на
умножается на  , то есть
, то есть
 .
.
Правило 1. Если  есть
есть  , то частное решение
, то частное решение  надо искать в виде
надо искать в виде
 ,
,
где 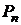 – многочлен
– многочлен  -й степени, а
-й степени, а  – кратность корня
– кратность корня  . Для вычисления неопределенных коэффициентов
. Для вычисления неопределенных коэффициентов  надо подставить
надо подставить  в (8) и затем приравнять коэффициенты при одинаковых степенях
в (8) и затем приравнять коэффициенты при одинаковых степенях  .
.
Пример.
 ,
,  , корень
, корень  – однократный, тогда
– однократный, тогда
 ,
,

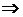
 ,
,  ,
,  и
и
 .
.
Случай 2.
 ,
,  ,
,
 . (*)
. (*)
Сделаем замену 
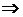
 ,
, 
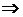

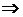
 , где
, где
 ,
,  .
.
Таким образом, уравнение (*) сведено к частному случаю, рассмотренному выше. Следовательно:
1. Если  , тогда
, тогда 
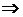
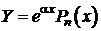 , где коэффициенты
, где коэффициенты  следует определить.
следует определить.
2.  ,
,  , то есть если
, то есть если  – простой корень характеристического уравнения, то
– простой корень характеристического уравнения, то 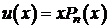
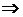
 .
.
3.  , то есть
, то есть  – двойной корень характеристического уравнения, то
– двойной корень характеристического уравнения, то 
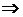
 .
.
Правило 2.
Если  , то
, то
 ,
,
где  – кратность корня
– кратность корня  в характеристическом уравнении.
в характеристическом уравнении.
Пример.
 ,
,

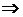

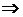
 и
и  .
.
 , подставляя в дифференциальное уравнение, получим:
, подставляя в дифференциальное уравнение, получим:
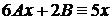
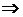
 ,
,  ,
,  .
.
 .
.
Перейдем теперь к общему случаю:
 .
.
 2018-02-14
2018-02-14 997
997








