Линейные дифференциальные уравнения 2-го порядка содержат все основные, типичные черты уравнений  -го порядка.
-го порядка.
Однородное линейное дифференциальное уравнение  -го порядка имеет вид:
-го порядка имеет вид:
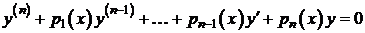 . (1)
. (1)
Для него, как и для линейного дифференциального уравнения 2-го порядка, справедливы теоремы о частных решениях 1 и 2. То есть линейные комбинации частных решений также являются решениями и если известно одно или несколько решений, то можно понизить порядок на одну или более единиц.
Определение. Фундаментальной системой решений уравнения (1) называется всякая система  частных решений
частных решений 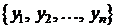 , которая обладает следующим свойством: ни при каких
, которая обладает следующим свойством: ни при каких  ,
,  , одновременно не равных нулю, линейная комбинация
, одновременно не равных нулю, линейная комбинация
 . (а)
. (а)
В этом случае  , удовлетворяющие (а), называют линейно независимыми.
, удовлетворяющие (а), называют линейно независимыми.
Из определения ледует, что нулевое решение не входит в фундаментальную систему решений. Например,  ,
,  . Тогда, положив
. Тогда, положив  , …,
, …,  , получим
, получим
 ,
,
что противоречит определению фундаментальной системы решений. Таким образом, фундаментальная система решений не может содержать ни одного  . При
. При  новое определение тождественно старому.
новое определение тождественно старому.
Далее, вронскиниан фундаментальной системы решений (и только фундаментальной системы решений) отличен от тождественного нуля. Вронскиниан в общем случае имеет вид:
 .
.
Формула Остроградского-Лиувилля также имеет место в общем случае:
 .
.
Из нее также следует, что  либо тождественно равен нулю, либо не равен нулю ни при каком
либо тождественно равен нулю, либо не равен нулю ни при каком  . Первый случай соответствует не фундаментальной системе решений, второй – фундаментальной системе решений.
. Первый случай соответствует не фундаментальной системе решений, второй – фундаментальной системе решений.
Существование фундаментальной системы решений доказывается аналогично дифференциальному уравнению 2-го порядка. Основная теорема устанавливает, что общее решение однородного линейного дифференциального уравнения  -го порядка имеет вид:
-го порядка имеет вид:
 , где
, где  .
.
Неоднородное линейное дифференциальное уравнение  -го порядка имеет вид:
-го порядка имеет вид:
 .
.
Теоремы о частных решениях справедливы и в эом случае. Также, как и метод Лагранжа вариации произвольных постоянных:

Однородное линейное дифференциальное уравнение  -го порядка с постоянными коэффициентами имеет вид:
-го порядка с постоянными коэффициентами имеет вид:
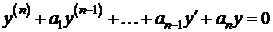 ,
,
 .
.
Любому действительному  -кратному корню
-кратному корню  соответствуют решения:
соответствуют решения:
 ,
,  ,
,  .
.
Так как  – действительные числа, то комплексные корни характеристического уравнения встречаются только сопряженными парами и имеют одинаковую кратность. Любой паре
– действительные числа, то комплексные корни характеристического уравнения встречаются только сопряженными парами и имеют одинаковую кратность. Любой паре  кратности
кратности  соответствует
соответствует  частных решений:
частных решений:
 ,
,  , …,
, …, 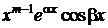 ,
,
 ,
,  , …,
, …,  .
.
Таким образом, в общем случае решение однородного линейного дифференциального уравнения  -го порядка имеет вид:
-го порядка имеет вид:
 ,
,
где  и
и  – кратности корней, а
– кратности корней, а  ,
,  ,
,  – многочлены соответствующих степеней.
– многочлены соответствующих степеней.
И, наконец, 2 теоремы о приведении к дифференциальным уравнениям с постоянными коэффициентами.
Теорема 1.
Если линейное дифференциальное уравнение  -го порядка
-го порядка
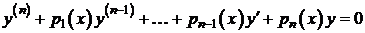 (*)
(*)
допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи замены независимой переменной  вида
вида  , то такой цели служит только подстановка
, то такой цели служит только подстановка
 , где
, где  .
.
Теорема 2.
Если (*) допускает приведение к дифференциальному уравнению с постоянными коэффициентами при помощи подстановки  , преобразующей неизвестную функцию
, преобразующей неизвестную функцию  , то такое преобразование выполняется только, если положить
, то такое преобразование выполняется только, если положить

Для неоднородных линейных дифференциальных уравнений приведение осуществляется по тем же формулам.
 2018-02-14
2018-02-14 2089
2089

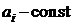 ,
,