Тема 8. Динамические эконометрические модели

Можно выделить два основных типа динамических эконометрических моделей. К моделям первого типа относятся модели ав­торегрессии и модели с распределенным лагом, в которых значе­ния переменной за прошлые периоды времени (лаговые пере­менные) непосредственно включены в модель. Модели второго типа учитывают динамическую информацию в неявном виде. В эти модели включены переменные, характеризующие ожидае­мый или желаемый уровень результата, или одного из факторов в момент времени t. Этот уровень считается неизвестным и опреде­ляется экономическими единицами с учетом информации, кото­рой они располагают в момент (t — 1).

В зависимости от способа определения ожидаемых значений показателей различают модели неполной корректировки, адап­тивных ожиданий и рациональных ожиданий. Оценка парамет­ров этих моделей сводится к оценке параметров моделей авторе­грессии.

Эконометрическое моделирование охарактеризованных вы­ше процессов осуществляется с применением моделей, содержа­щих не только текущие, но и лаговые значения факторных пере­менных. Эти модели называются моделями с распределенным лагом. Модель вида 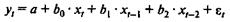является примером модели с распределенным лагом.

Наряду с лаговыми значениями независимых, или фактор­ных, переменных на величину зависимой переменной текущего периода могут оказывать влияние ее значения в прошлые момен­ты или периоды времени. Например, потребление в момент вре­мени t формируется под воздействием дохода текущего и преды­дущего периодов, а также объема потребления прошлых перио­дов, например потребления в период (t — 1). Эти процессы обыч­но описывают с помощью моделей регрессии, содержащих в ка­честве факторов лаговые значения зависимой переменной, кото­рые называются моделями авторегрессии. Модель вида относится к моделям авторегрессии.

Рассмотрим модель с распределенным лагом в ее общем виде в предположении, что максимальная величина лага конечна:

 

Эта модель говорит о том, что если в некоторый момент вре­мени t происходит изменение независимой переменной x_t то это изменение будет влиять на значения переменной у в течение l следующих моментов времени.

Коэффициент регрессии b ₀ при переменной x_t характеризует среднее абсолютное изменение y_t при изменении x_t на 1 ед. свое­го измерения в некоторый фиксированный момент времени t, без учета воздействия лаговых значений фактора х. Этот коэффици­ент называют краткосрочным мультипликатором.

В момент (t + 1) совокупное воздействие факторной перемен­ной x_t на результату, составит (b_о + b₁) усл. ед., в момент (t+2) это воздействие можно охарактеризовать суммой (b_о + b₁ + b₂) и т. д. Полученные таким образом суммы называют промежуточными мультипликаторами.

С учетом конечной величины лага можно сказать, что изме­нение переменной x_t в момент t на 1 усл. ед. приведет к общему изменению результата через / моментов времени на (b _о + b ₁ +...+ b_l) абсолютных единиц.

Введем следующее обозначение:

b_о + b ₁+...+ b_l = b.

Величину b называют долгосрочным мультипликатором. Он по­казывает абсолютное изменение в долгосрочном периоде t + l ре­зультата у под влиянием изменения на 1 ед. фактора х.

Предположим β j = bj/b,j = O:l.

Назовем полученные величины относительными коэффициен­тами модели с распределенным лагом. Если все коэффициенты b_j имеют одинаковые знаки, то для любого j

О < β_j; < 1 и

В этом случае относительные коэффициенты β_j являются ве­сами для соответствующих коэффициентов b _j. Каждый из них из­меряет долю общего изменения результативного признака в мо­мент времени (t+j).

Зная величины β_j, с помощью стандартных формул можно определить еще две важные характеристики модели множествен­ной регрессии: величину среднего лага и медианного лага. Сред­ний лаг определяется по формуле средней арифметической взве­шенной:

и представляет собой средний период, в течение которого будет происходить изменение результата под воздействием изменения фактора в момент времени t. Небольшая величина среднего лага свидетельствует об относительно быстром реагировании резуль­тата на изменение фактора, тогда как высокое его значение гово­рит о том, что воздействие фактора на результат будет сказывать­ся в течение длительного периода времени. Медианный лаг — это величина лага, для которого

Это тот период времени, в течение которого с момента време­ни t будет реализована половина общего воздействия фактора на результат.

Применение обычного МНК к таким моделям в большинстве случаев затруднительно по следующим причинам.

Во-первых, текущие и лаговые значения независимой пере­менной, как правило, тесно связаны друг с другом. Тем самым оценка параметров модели проводится в условиях высокой мультиколлинеарности факторов.

Во-вторых, при большой величине лага снижается число на­блюдений, по которому строится модель, и увеличивается число ее факторных признаков. Это ведет к потере числа степеней сво­боды в модели.

В-третьих, в моделях с распределенным лагом часто возни­кает проблема автокорреляции остатков. Вышеуказанные обсто­ятельства приводят к значительной неопределенности относи­тельно оценок параметров модели, снижению их точности и по­лучению неэффективных оценок. Чистое влияние факторов на результат в таких условиях выявить невозможно. Поэтому на практике параметры моделей с распределенным лагом проводят в предположении определенных ограничений на коэффициенты регрессии и в условиях выбранной структуры лага.

Обратимся теперь к модели авторегрессии. Пусть имеется следующая модель:

Как и в модели с распределенным лагом, b₀ в этой модели ха­рактеризует краткосрочное изменение y_t под воздействием изме­нения х_t на 1 ед. Однако промежуточные и долгосрочный мульти­пликаторы в моделях авторегрессии несколько иные. К моменту времени (t + 1) результат изменился под воздействием измене­ния изучаемого фактора в момент времени t на 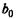ед., а под воздействием своего изменения в непосредственно предшеству­ющий момент времени — на с₁ ед. Таким образом, общее абсо­лютное изменение результата в момент (t + 1) составит ед. Аналогично в момент времени (t + 2) абсолютное изменение ре­зультата составит ед. и т. д. Следовательно, долгосрочный мультипликатор в модели авторегрессии можно рассчитать как сумму краткосрочного и промежуточных мультипликаторов:

Учитывая, что практически во все модели авторегрессии вво­дится так называемое условие стабильности, состоящее в том, что коэффициент регрессии при переменной по абсолютной ве­личине меньше единицы(|c₁| < 1), соотношение (7.8) можно преоб­разовать следующим образом:

 

где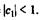

Отметим, что такая интерпретация коэффициентов модели авторегрессии и расчет долгосрочного мультипликатора основа­ны на предпосылке о наличии бесконечного лага в воздействии текущего значения зависимой переменной на ее будущие зна­чения.

Процедура применения метода Алмон для расчета параметров модели с распределенным лагом выглядит следующим образом.

1.  Определяется максимальная величина лага l.

2. Определяется степень полинома к, описывающего структуру лага.

3. По соотношениям (7.14) рассчитываются значения переменных z ₀,..., z _k.

4. Определяются параметры уравнения линейной регрессии (7.15).

5.С помощью соотношений (7.11) рассчитываются парамет­ры исходной модели с распределенным лагом.

Применение метода Алмон сопряжено с рядом проблем.

Во-первых, величина лага l должна быть известна заранее. При ее определении лучше исходить из максимально возможного ла­га, чем ограничиваться лагами небольшой длины. Выбор мень­шего лага, чем его реальное значение, приведет к тому, что в мо­дели регрессии не будет учтен фактор, оказывающий значитель­ное влияние на результат, т. е. к неверной спецификации модели. Влияние этого фактора в такой модели будет выражено в остат­ках. Тем самым в модели не будут соблюдаться предпосылки МНК о случайности остатков, а полученные оценки ее параметров окажутся неэффективными и смещенными. Выбор большей величины лага по сравнению с ее реальным значением будет оз­начать включение в модель статистически незначимого фактора и снижение эффективности полученных оценок, однако эти оценки все же будут несмещенными.

Существует несколько практических подходов к определению реальной величины лага, например построение нескольких урав­нений регрессии и выбор наилучшего из этих уравнений или применение формальных критериев, например критерия Шварца. Однако наиболее простым способом является измерение тесноты связи между результатом и лаговыми значениями фактора. Кроме того, оптимальную величину лага можно приближенно опреде­лить на основе априорной информации экономической теории или проведенных ранее эмпирических исследований.

Во-вторых, необходимо установить степень полинома к. Обычно на практике ограничиваются рассмотрением полиномов 2-й и 3-й степени, применяя следующее простое правило: вы­бранная степень полинома к должна быть на единицу больше числа экстремумов в структуре лага. Если априорную информа­цию о структуре лага получить невозможно, величину к проще всего определить путем сравнения моделей, построенных для различных значений k, и выбора наилучшей модели.

В-третьих, переменные z, которые определяются как линей­ные комбинации исходных переменных х, будут коррелировать между собой в случаях, когда наблюдается высокая связь между самими исходными переменными. Поэтому оценку параметров модели приходится проводить в условиях мультиколлинеарности факторов. Однако мультиколлинеарность факторов z₀,..., Z_k в модели сказывается на оценках параметров b₀,..., b _l в несколько меньшей степени, чем если бы эти оценки были полу­чены путем применения обычного МНК непосредственно к мо­дели в условиях мультиколлинеарности факторов xt..., xt-l. Это связано с тем, что в модели мультиколлинеарность ве­дет к снижению эффективности оценок с₀,..., с_k поэтому каждый из параметров b ₀,..., b_l которые определяются как линейные ком­бинации оценок c ₀,..., с_к, будет представлять собой более точную оценку, а стандартные ошибки этих параметров не будут превы­шать стандартные ошибки параметров, полученных по модели обычным МНК.

Метод Алмон имеет два неоспоримых преимущества.

• Он достаточно универсален и может быть применен для моделирования процессов, которые характеризуются разнообразными структурами лагов.

• При относительно небольшом количестве переменных (обычно выбирают к = 2 или к = 3), которое не приво­дит к потере значительного числа степеней свободы, с помо­щью метода Алмон можно построить моде ли с распределенным лагом любой длины.

Рассмотренные выше модели были построены в предположе­нии конечной величины лага /. Предположим теперь, что для описания некоторого процесса используется модель с бесконеч­ным лагом вида: y_t = а = b _о -x_t + b ₁ ·x_t-1 + b ₂ ·x_t-2 +... +

Очевидно, что параметры такой модели обычным МНК или с помощью иных стандартных статистических методов определить нельзя, поскольку модель включает бесконечное число фактор­ных переменных. Однако, приняв определенные допущения от­носительно структуры лага, оценки ее параметров все же можно получить. Эти допущения состоят в наличии геометрической структуры лага, т. е. такой структуры, когда воздействия лаговых значений фактора на результат уменьшаются с увеличением ве­личины лага в геометрической прогрессии.

Впервые изложенный в этом разделе подход к оценке параме­тров моделей с распределенным лагом типа (7.16) был предложен Л.М. Койком. Койк предположил, что существует некоторый постоянный темп λ (0 < λ < 1) уменьшения во времени лаговых воздействий фактора на результат. Если, например, в период /ре­зультат изменялся под воздействием изменения фактора в этот же период времени на b₀ ед., то под воздействием изменения фак­тора, имевшего место в период (t — 1), результат изменится на b₀ · λ ед.; в период (t - 2) - на b₀ · λ · λ = b₀ · λ ед., и т. д. Для не­которого периода (t — l) это изменение результата составит b₀ · λ ед. В более общем виде можно записать:

b_j = b₀ λ; j = 0, 1,2,..., 0<λ<1.

Ограничение на значения λ > 0 обеспечивает одинаковые зна­ки для всех коэффициентов b_j > 0, а ограничение λ < 1 означает, что с увеличением лага значения параметров модели  убы­вают в геометрической прогрессии. Чем ближе λ к 0, тем выше темп снижения воздействия фактора на результат во времени и тем большая доля воздействия на результат приходится на теку­щие значения фактора х_t

Описанный выше алгоритм получил название преобразова­ния Койка. Это преобразование позволяет перейти от модели с бесконечными распределенными лагами к модели авторегрес­сии, содержащей две независимые переменные x_t и y_t-₁.

Одним из возможных методов расчета параметров уравнения авторегрессии является метод инструментальных переменных. Сущность этого метода состоит в том, чтобы заменить перемен­ную из правой части модели, для которой нарушаются предпо­сылки МНК, на новую переменную, включение которой в модель регрессии не приводит к нарушению его предпосылок. Примени­тельно к моделям авторегрессии необходимо удалить из правой части модели переменную , Искомая новая переменная, кото­рая будет введена в модель вместо , должна иметь два свойст­ва. Во-первых, она должна тесно коррелировать с , во-вторых, она не должна коррелировать с остатками .