2018-02-14
1090
Конспект лекции: Эконометрика как наука расположена где-то между экономикой, статистикой и математикой. Эконометрика – это наука, связанная с эмпирическим выводом экономических законов. То есть мы используем данные или «наблюдения» для того, чтобы получить количественные зависимости для экономических соотношений.
Во всей этой деятельности существенным является использование моделей. Можно выделить три основных класса моделей, которые применяются для анализа и/или прогноза: модели временных рядов; регрессионные модели с одним уравнением; системы одновременных уравнений. Если модель содержит только одну объясняющую переменную, т.е. k=1, она называется парной регрессией. При k>1 мы имеем дело с множественной регрессией.
Основу эконометрического моделирования составляют статистические данные. Их различают по типам. Перекрестные данные собираются по какому-либо экономическому показателю для разных объектов(фирм, стран, домохозяйств) в один момент времени или в разные моменты в случае, когда время несущественно. Временные ряды – данные для одного объекта в различные моменты времени. Промежуточное положение занимают панельные данные, которые отражают наблюдения по большому числу объектов за небольшое число моментов времени, например,прибыли предприятий Казахстана за последние три года.
|
|
|
Случайной переменной называется переменная, которая с определенной вероятностью может принимать значения из каждого заданного множества.
Различают дискретные и непрерывные случайные величины. Если случайная величина может принимать конечное или счетное число значений, то это дискретная случайная величина. Пример – сумма выпавших очков при бросании двух игральных костей; число телевизоров, проданных в магазине за один день. Ее можно задать в виде таблицы
| x |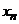 
| 
| …. | 
|
| p | 
| 
| …. | 
|
где , , … 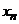- все значения, которые может принимать случайная величина х с вероятностями … соответственно.
При этом 
. 
Случайная величина, которая может принимать любые значения из некоторого интервала, является непрерывной случайной величиной. Пример –температура в комнате; максимальный биржевой курс доллара на торгах в течение дня. Она задается функцией плотности вероятности, принимающей неотрицательные значения.
Вероятность попадания случайной величины х в интервал [а,b] равна
.
Эта площадь под кривой плотности вероятности 
на отрезке a,b. Поскольку какое-либо значение х реализуется, то 
.
Особое значение имеет нормальное распределение вероятности.
Центральная предельная теорема утверждает, что если случайную величину можно представить как сумму большого числа не зависящих друг от друга слагаемых, каждое из которых вносит в сумму незначительный вклад, то эта сумма распределена приблизительно по нормальному закону.
|
|
|
Математическое ожидание случайной величины. Свойства математического ожидания. Математическое ожидание дискретной случайной величины – это взвешенное среднее всех ее возможных значений на вероятность соответствующего исхода. Математически если случайную величину обозначить как х, то ее математическое ожидание будет обозначаться как 
.
Предположим, что х может принимать n конкретных значений (
) и что вероятность получения 
равна 
. Тогда математическое ожидание дискретной случайной величины равна
(1)
и непрерывной случайной величины: 
.
Например для распределения
| х | 1 | 3 | 5 |
| р | 0,3 | 0,5 | 0,2 |
Математическое ожидание Е(х)= 1*0,3+3*0,5*5*0,2=2,8.
Математическое ожидание случайной величины называют ее средним по генеральной совокупности. Совокупность всех возможных значений случайной переменной описывается генеральной совокупностью, из которой извлекаются эти значения. Для случайной величины х это значение часто обозначатся как 
.
Свойства 1. Математическое ожидание суммы случайных величин равно сумме их математических ожиданий, т.е.
(2)
Свойства 2. Если случайная переменная умножается на константу, то ее математическое ожидание умножается на ту же константу. Если х – случайная переменная и а – константа, то
(3)
Свойства 3. Математическое ожидание константы есть сама эта величина, т.е.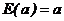 
Теоретическая дисперсия Дисперсией (теоретической) случайной величины х называется математическое ожидание квадрата отклонения х от математического ожидания 
, т.е.
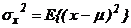(4)
следовательно, для дискретной случайной величины
,
а для непрерывной случайной величины
.
Пример расчета дисперсии для дискретной случайной величины 
, 
.
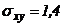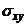-теоретическое стандартное отклонение вычисляется путем простого извлечения из нее квадратного корня.
Положительное значение 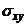свидетельствует о наличии прямой статистической связи между х,у, а отрицательное значение 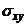- об обратной статистической связи между х,у.
Вероятность в непрерывном случае.
Дискретные случайные переменные по определению принимают значения из некоторого конечного набора. Каждое из этих значений связано с определенной вероятностью, характеризующей его «вес». Если эти «веса» известны, то не составит труда рассчитать теоретическое среднее(математическое ожидание) и дисперсию.
Вы можете представить указанные «веса» как определенные количества «пластичной массы», равные вероятностям соответствующих значений. Сумма вероятностей и, следовательно, суммарный «вес» этой массы равен «единице».
Более подробно рассмотрим анализ для непрерывных случайных величин, которые могут принимать бесконечное число значений.
Проиллюстрируем наши рассуждения на примере температуры в комнате. Для определенности предположим, что меняется в пределах от 55 до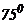 
по Фаренгейту, и вначале допустим, что значения в этом диапазоне равновероятны.(рисунок 1).
 |
|
|
|
|
В этом примере, мы будем предполагать, что «пластичная масса размазана» на единичной площади. Это связано с тем совокупная вероятность всегда равняется единице. В данном случае наша «масса» покрыла прямоугольник, и поскольку основание этого прямоугольника равно 20, его высота определяется из соотношения: 20 х Высота=1, так как произведение основания и высоты равно площади. Следовательно, высота равна 0,05.
Найдя высоту прямоугольника, мы можем ответить на вопросы типа: с какой вероятностью температура будет находиться в диапазоне от 65 до 
F? Ответ определяется величиной «замазанной» площади, лежащей в диапазоне от 65 до F, представленной заштрихованной фигурой на рисунке 2. Основание прямоугольника равно 5, его высота равна 0,05 и, соответственно, площадь –0,25. Искомая вероятность равна 
, что в любом случае очевидно, поскольку промежуток от 65 до F составляет всего диапазона.
|
Высота заштрихованной площади представляет то, что формально называется плотностью вероятности в той точке, и если эта высота может быть записана как функция значений случайной переменной, то эта функция называется функцией плотности вероятности. В нашем примере она записывается как 
, где х -температура, и 
.
В качестве первого приближения функция плотности вероятности показывает вероятность нахождения случайной переменной внутри единичного интервала вокруг данной точки. В нашем примере эта функция всюду равна 0,05, откуда вытекает, что температура находится, например, между 60 и 
F с вероятностью 0,05.
В нашем случае график функции плотности вероятности горизонтален, и ее указанная интерпретация точна, однако в общем случае эта функция непрерывно меняется, и ее интерпретация дает лишь приближение. Далее мы рассмотрим пример, когда эта функция непостоянна, поскольку не все температуры равновероятны. Предположим, что центральное отопление работает таким образом, что температура никогда не падает ниже 
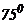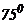F, а в жаркие дни температура превосходит этот уровень, не превышая, как и ранее, F. Мы будем считать, что плотность вероятности максимальна при температуре F и далее она равномерно убывает до нуля при F.
|
|
|
Общая «замазанная» площадь равен единице, поскольку совокупная вероятность равна единице. Площадь треугольника равна половине произведения основания на высоту, получаем: 
х 10 х Высота =1 и высота при F равна 0,20.
Предположим вновь, что мы хотим знать вероятность нахождения температуры в промежутке между 65 и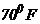 
. Она представлена заштрихованной площадью на рисунке 3, и равна 0,75. Если вы предпочитаете процентное измерение, то это означает, что с вероятностью 75% температура попадает в диапазон 65 - 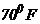и только с вероятностью 25%- в диапазон 70- 
.
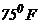В данном случае функция плотности вероятности равна 
.
|
Основная литература: 1[3-8]
Дополнительная литература: 1[5-6]
Контрольные вопросы:
1.Дайте определение эконометрики.
2.Приведите основные типы статистических данных.
3.Дайте определение случайной величины.
4. Какой типичный вид графика функции плотности вероятности непрерывной случайной величины.
5.Дайте определение математическому ожиданию.
6.Дайте определение функции плотности вероятности.
Тема лекции 2.Постоянная и случайная составляющие случайной переменной. Несмещенность. Эффективность. Состоятельность. Выборочная ковариация. Дисперсия. Коэффициент корреляция
Конспект лекции: Часто вместо рассмотрения случайной величины как единого целого можно и удобно разбить ее на постоянную и чисто случайно составляющие, где постоянная составляющая всегда есть ее математическое ожидание. Если х – случайная переменная и m - ее математическое ожидание, то декомпозиция случайной величины записывается следующим образом: 
, где u – чисто случайная составляющая.
Случайная составляющая u определяется как разность между х и m: 
. Из определения следует, что математическое ожидание величины u равно нулю, а теоретическая дисперсия х равна теоретической дисперсии u.
Способы оценивания и оценки. До сих пор мы предполагали, что имеется точная информация о рассматриваемой случайной переменной, в частности – об ее распределении вероятностей или функции плотности распределения. С помощью этой информации можно рассчитать теоретическое математическое ожидание, дисперсию и любые другие характеристики.
Однако на практике, за исключением искусственно простых случайных величин мы не знаем точного вероятностного распределения или плотности распределения вероятностей. Это означает, что неизвестны также и теоретическое математическое ожидание, и дисперсия. Мы, тем не менее, можем нуждаться в оценках этих или других теоретических характеристик генеральной совокупности.
Процедура оценивания всегда одинакова. Берется выборка из n наблюдений, и с помощью подходящей формулы рассчитывается оценка нужной характеристики.Способ оценивания – это общее правило, или формула, в то время как значение оценки – это конкретное число, которое меняется от выборки к выборке.
Приведем формулы оценивания для двух важнейших характеристик генеральной совокупности:
выборочное среднее - 
;
выборочное дисперсия случайной величины - 
.
Оценки как случайные величины. Несмещенность. Эффективность. Состоятельность
Получаемая оценка представляет частный случай случайной переменной. Причина здесь в том, что сочетание значений х в выборке случайно, поскольку х- случайная переменная и, следовательно, случайной величиной является и функции набора ее значений. Возьмем, например 
- оценку математического ожидания:
(5)
Мы только, что показали, что величина х а i-м наблюдении может быть разложен на две составляющие: постоянную часть m и чисто случайную составляющую ui:
(6)
Следовательно, 
(7)
где 
-выборочное среднее величин ui.
Отсюда можно видеть, что , подобно х, имеет фиксированную, та и чисто случайную составляющие. Ее фиксированная составляющая -m, то есть математическое ожидание х, а ее случайная составляющая - , то есть среднее значение чисто случайной составляющей в выборке.
Величина 
- оценка теоретической дисперсии х – также является случайной переменной. Вычитая (7) из (6), имеем:
(8)
следовательно,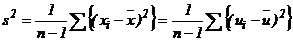 
.
Таким образом, s2 зависит от чисто случайной составляющей наблюдений х в выборке.
Полученная тем или иным способом оценка характеристики случайной величины сама является случайной величиной, так как она основывается на случайных реализациях переменной.
Оценка характеристики случайной величины называется несмещенной, если ее математическое ожидание совпадает с теоретическим значением этой характеристики.
Например, оценкой для математического ожидания может может служить среднее выборочное . Имеем 
.
Значит, - несмещенная оценка для математического ожидания m случайной величины х.
Эффективная оценка – это та, у которой дисперсия минимальна. Сейчас мы рассмотрим дисперсию обобщенной оценки теоретического среднего и покажем, что она минимальна в том случае, когда оба наблюдения имеют равные веса.
Если наблюдения 
и 
независимы, теоретическая дисперсия обобщенной оценки равна:
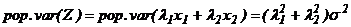(9)
Мы уже выяснили, что для несмещенности оценки необходимо равенство единице суммы 
и 
. Следовательно, для несмещенных оценок 
и
Поскольку мы хотим выбрать так, чтобы минимизировать дисперсию, нам нужно минимизировать при этом (
). Минимум достигается при 
. Следовательно, =0.5.
Итак, мы показали, выборочное среднее имеет наименьшую дисперсию среди оценок рассматриваемого типа. Это означает, что оно имеет наиболее «сжатое» вероятностное распределение вокруг истинного среднего и, следовательно наиболее точно. Строго говоря, выборочное среднее – это наиболее эффективная оценка среди всех несмещенных оценок.
Если предел оценки по вероятности равен истинному значению характеристики генеральной совокупности, то эта оценка называется состоятельной.
Тот факт, что при увеличении размера выборки распределение становится симметричным вокруг истинного значения, указывает на асимптотическую несмещенность. То, что в конечном счете оно превращается в единственную точку истинного значения, говорит о состоятельности оценки.
Выборочная ковариация. Дисперсия. Коэффициент корреляция
Выборочная ковариация является мерой взаимосвязи между двумя переменными.
При наличии n наблюдений двух переменных (х и у) выборочная ковариация между х и у задается формулой:
. (10)
Правила расчета ковариации.
1. Если 
, то 
.
2. Если 
, где а – константа, то 
.
3. Если 
, где а – константа, то 
.
Пример. В период между 1963 и 1972 потребительский спрос на бензин устойчиво повышался. Эта тенденция прекратилась в 1973г., а затем последовали нерегулярные колебания спроса с незначительным его падением в целом. В табл. Приведены данные о потребительском спросе и реальных ценах после нефтяного кризиса. На рисунке 4 эти данные показаны в виде диаграммы рассеяния. Можно видеть некоторую отрицательную связь между потребительским спросом на бензин и его реальной ценой.
| год | расходы | Индеск реальных цен |
| 1973 | 26,2 | 103,5 |
| 1974 | 24,8 | 127,0 |
| 1975 | 25,6 | 126,0 |
| 1976 | 26,8 | 124,8 |
| 1977 | 27,7 | 124,7 |
| 1978 | 28,3 | 121,6 |
| 1979 | 27,4 | 149,7 |
| 1980 | 25,1 | 188,8 |
| 1981 | 25,2 | 193,6 |
| 1982 | 25,6 | 173,9 |
Показатель выборочной ковариации позволяет выразить данную связь единичным числом. Для его вычисления мы сначала находим средние значения цены и спроса на бензин. Обозначив через р и спрос – через у, определяем 
и 
, которые для выборки оказываются равными соответственно 143,36 и 26,27. Затем для каждого года вычисляем отклонение величин р и у от средних и перемножаем их. Для первого года (р- 
) равно (103,5-143,36) или –39,86 и (у- ) составит 2.79. Проделаем это для всех годов выборки и возьмем среднюю величину, она и будет выборочной ковариацией.
Средняя величина (-16,24) она является значением выборочной ковариации. В данном случае она отрицательна. Так это и должно быть. Отрицательная связь, как это имеет место в данном примере выражается отрицательной ковариацией, а положительная связь – положительной ковариацией.
Диаграмму рассеяния (рис)наблюдений делится на четыре части вертикальной и горизонтальной линиями, проведенными через и соответственно. Пересечение этих линий образует точку (, ), которая показывает среднюю цену и средний спрос за период времени, соответствующий нашей выборке.
Для любого наблюдения, лежащего в квадранте А, значения реальной цены и спроса выше соответствующих средних значений. Для данных наблюдений как (р- ), так и (у- ) являются положительными, а поэтому должно быть положительным и (р- )(у- ),.
| наблюдение | у | р | (р- )
| (у- )
| (р- ) (у- )
|
| 1973 | 26,2 | 103,5 | -39,86 | -0,07 | 2,79 |
| 1974 | 24,8 | 127,0 | -16,36 | -1,47 | 24,05 |
| 1975 | 25,6 | 126,0 | -17,36 | -0,67 | 11,63 |
| 1976 | 26,8 | 124,8 | -18,56 | 0,53 | -9,84 |
| 1977 | 27,7 | 124,7 | -18,66 | 1,43 | -26,68 |
| 1978 | 28,3 | 121,6 | -21,76 | 2,03 | -44,17 |
| 1979 | 27,4 | 149,7 | 6,34 | 1,13 | 7,16 |
| 1980 | 25,1 | 188,8 | 45,44 | -1,17 | -53,16 |
| 1981 | 25,2 | 193,6 | 50,24 | -1,07 | -53,76 |
| 1982 | 25,6 | 173,9 | 30,54 | -0,67 | -20,46 |
| Сумма Среднее | 262,7 26,27 | 1433,6 143,36 | -162,44 -16,24 |
|
|
5956
5760