Метод наименьших квадратов

Одним из важных практических применений экстремума функции нескольких переменных является метод наименьших квадратов.

Пусть в результате некоторого опыта или наблюдения установлена зависимость между переменными величинами х и у, выражаемая в виде таблицы:

 

х	х1	х2	…	хn
у	у1	у2	…	уn

 

Пусть требуется перейти от табличного метода задания функции к аналитическому (т.е. выраженному в виде формулы), причем, если это нельзя сделать точно, постараемся получить аналитическую связь приближенно.

Теперь обратимся к графическому изображению данной системы. Рассматривая значения х и у как координаты точек в прямоугольной системе координат, наносим эти точки на график. Пусть, например построенные точки расположились достаточно близко к некоторой прямой. Поэтому можно приблизительно считать, что между х и у существует линейная зависимость, выражаемая формулой,

у = ах + b.

Поставим задачу аналитического определения неизвестных коэффициентов а и b.

В основе аналитического метода определения а и b лежит метод наименьших квадратов. Точки, полученные на основании опытных данных, вообще говоря, не лежат на искомой прямой. Если бы некоторая точка (х_i, у_i) лежала на прямой, то ее координаты удовлетворяли бы уравнению прямой, т.е. имело бы место равенство:

у_i = ax_i + b   или    ax_i + b - y_i = 0

Однако в общем случае подстановка координат точки в уравнение прямой дала бы:

ax_i + b - y_i = ε_i,

где ε_i ─ какая то малая величина.

Для первой точки получаем

ax₁ + b - y₁ = ε₁,

Для второй точки

ax₂ + b - y₂ = ε₂, и т.д.

Для последней точки

ax_n + b - y_n = ε_n.

Величины ε₁, ε₂, …, ε_n характеризуют отклонения рассматриваемых точек от точек искомой прямой: они выражают отклонения ординат точек наблюдения от ординат точек искомой прямой.

Метод наименьших квадратов требует подобрать значения параметров а и b таким образом, чтобы сумма квадратов отклонения ε_i, была при этом наименьшей, т.е.

Здесь x₁, x₂,..., x_n, y₁, y₂,..., y_n - заданные числа. Функция S есть функция двух независимых переменных a и b, т.е.:

S = f (a, b).

Необходимые условия существования экстремума функции дают:

¶S / ¶a = 0;            ¶S / d¶b = 0.

Вычислим эти частные производные:

¶S / ¶a = 2 (ax₁ + b - y₁) x₁ + 2 (ax₂ + b - y₂) x₂ +... +

+ 2 (ax_n + b - y_n) x_n,

¶S / ¶b = 2 (ax₁ + b - y₁) · 1 + 2 (ax₂ + b - y₂) · 1 +... +

+ 2 (ax_n + b - y_n) · 1.

Приравнивая частные производные к нулю и сокращая на 2, получаем систему двух линейных уравнений с двумя неизвестными a и b:

(ax₁ + b - y₁) x₁ + (ax₂ + b - y₂) x₂ +... + (ax_n + b - y_n) x_n = 0,

(ax₁ + b - y₁) + (ax₂ + b - y₂) +... + (ax_n + b - y_n) = 0.

Раскрывая скобки, и после соответствующих преобразований получаем:

                  (1)

Эти уравнения называются стандартными уравнениями, решение которых дает искомые значения a и b.

Система (1) может быть для удобства переписана следующим образом:

 

1.5. Правила составления систем стандартных уравнений

Существует определенное правило составления системы стандартных уравнений:

1. Записывается исходное уравнение:

y = a + bx.

2. Перемножаются все члены уравнения на коэффициент при первом неизвестном и суммируются:

.

3. Далее перемножаются все члены уравнения на коэффициент при втором неизвестном и также суммируются:

 и т.д.

Итак, система стандартных уравнений для функции у = а + bx имеет вид:

Для параболы второй степени у = а + bх + сх² система стандартных уравнений имеет вид:

Для параболы третьей степени у = а + bх + сх² + dx³:

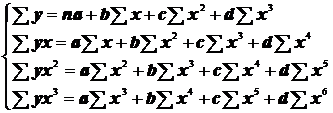
Для функции у = а +  система стандартных уравнений имеет вид:

Для функции у = 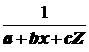  система стандартных уравнений записывается следующим образом:

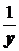  = а + bx + cZ

Для функции у = а + а₁х₁ + а₂х₂ + а₃х₃ система стандартных уравнений имеет вид:

Вопросы для самоконтроля

1. Дайте определение максимума, минимума функции в точке М₀ (х₀, у₀).

2. Сформулируйте необходимые условия для существования экстремума функции.

3. Сформулируйте, при каких обстоятельствах достигает функция максимума, минимума, при каких обстоятельствах остается вопрос открытым и требуются дополнительные исследования.

4. В чем экономический смысл уравнения связи? Как она выбирается?

5. При каких обстоятельствах используется метод неопределенных множителей Лагранжа?

6. В чем экономический смысл метода наименьших квадратов?

7. Каким образом определяются параметры системы? Например, а, b, c для функции

у = .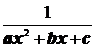

8. В чем экономический смысл величины ε₁, ε₂, …, ε_n в системе МНК? Всегда ли они имеют место?

9. Сформулируйте правило составления системы стандартных уравнений.

10. Составьте систему стандартных уравнений для следующих функций:

1. у = а - bx;                 2. y =  ;

3. y = a + bx + c 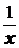 ;              4. y = ;

5. y = ;                        6. y = a · b^x;

7. y = a · x^b;                 8. y = a + a₁x₁ + a₂x₂.

 

Тест к главе 1 

1. Выберите неравенство, при котором функция достигает экстремума:

а)  АС - В² > 0;

б) АС - В² < 0;

в) АС - В² = 0;

     

2. Отметьте необходимые условия существования экстремума функции:

а) 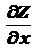> 0, > 0;

б) < 0, < 0;

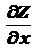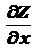в) = 0, = 0.

3. Укажите вспомогательную функцию Лагранжа:

а) Z = ƒ [x₁ + (x)] = F(x);

б)   Ф(х₁у) = ƒ(х₁у) + λφ(х₁у);

в) Ф(х₁у) = х +у + λ .

4. Укажите, правильно ли составлены системы стандартных уравнений:

а)

для функции у = а + bt;

б)

для функции  ;

в)

для функции у = а + а₁х₁ + а₂х₂.

5. Выберите привлекательные функции для прогнозирования:

а) у = а + bt;

б) у = аb^t;

в) .