Основное уравнение молекулярно-кинетической теории для давления, для температуры

Рассматривается идеальный газ, заключённый в сосуде. Каждая молекула, ударяясь о стенку, упруго отскакивает от неё и передаёт стенке импульс – это проявляется как давление газа на стенку. Получим выражение для давления газа при следующих предположениях:

1) все молекулы имеют одинаковые скорости v;

2) молекулы могут двигаться только в трёх взаимно перпендикулярных направлениях – либо параллельно стенке, либо перпендикулярно ей. В любой момент времени к стенке движется  часть всех молекул. Ещё  часть молекул движется от стенки;  молекул движется параллельно стенке (вверх или вниз на

Рис.6.2

рис.6.2) и последняя треть молекул – параллельно стенке и перпендикулярно плоскости рисунка 6.2. Число молекул, ударившихся о стенку площадью  за время , равно

,            (6.11)

так как за это время до стенки долетят молекулы, находящиеся от неё на расстоянии, не больше , то есть находящиеся в объёме . Каждая молекула при упругом столкновении передаёт стенке импульс 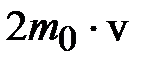. Тогда полный импульс, полученный стенкой за время , равен

.  (6.12)

По второму закону Ньютона в импульсной форме изменение импульса тела равно импульсу силы, действовавшей на тело:

,                                        (6.13)

тогда

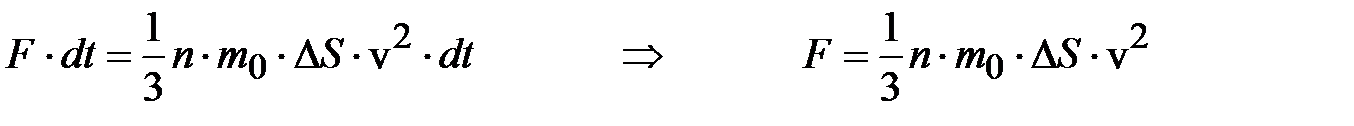    (6.14)

По определению давления:

.                                       (6.15)

В действительности скорости молекул неодинаковые, и все направления скоростей равновероятны. Но если при выводе формулы для давления всё это учесть, получится практически то же выражение; необходимо только заменить скорость  на среднюю квадратичную скорость , которая по определению равна

,                                            (6.16)

где N – полное число молекул; суммирование происходит по всем молекулам. Таким образом, давление газа равно

,                                        (6.17)

или

,                                           (6.18)

поскольку плотность .

Используя (6.17), выразим давление через среднюю кинетическую энергию поступательного движения молекул газа :

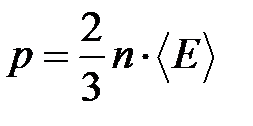.                                         (6.19)

Это – основное уравнение молекулярно-кинетической теории для давления.

Далее, из (6.17) и (6.6) получим выражение для средней квадратичной скорости молекул газа:

,

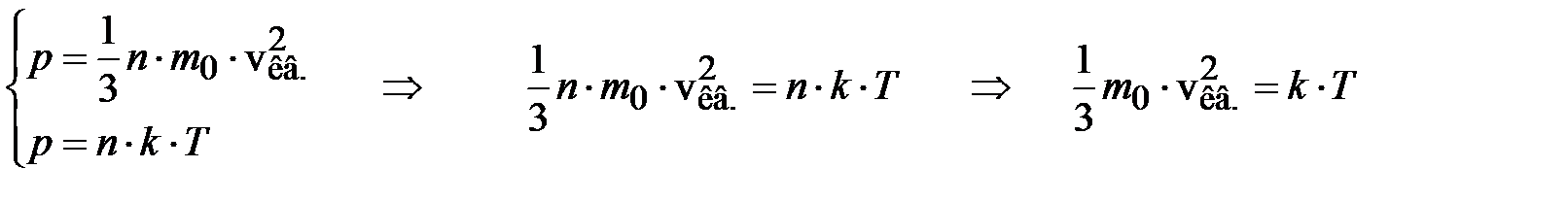или

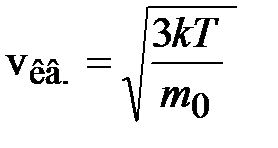;                                          (6.20)

.                              (6.20а)

Наконец, из (6.19) и (6.6) получим основное уравнение молекулярно-кинетической теории для температуры:

или

.                                            (6.21)

Именно это соотношение проясняет смысл абсолютной температуры: при абсолютном нуле (T =0 К) прекращается тепловое движение молекул, и именно поэтому абсолютный нуль недостижим. Соотношение (3.21) можно считать определением абсолютной температуры.

 

Билет