2018-02-14
1147
1. 
Пусть точка движется по окружности радиуса 
(рис.1.5). За время 
путь равен 
, угол поворота равен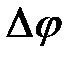 
. Угловое перемещение 
– вектор, направленный по оси вращения по правилу буравчика и равный углу поворота. Размерность 
.
Длина дуги и угол поворота связаны соотношением
, (1.22)
или
. (1.22а)
| Рис.1.5 |
: 
, отсюда 
, (1.23)
поскольку линейная скорость 
(1.5), а производная угла поворота по времени есть угловая скорость:
| Рис.1.6 |
. (1.24) Её физический смысл – угол поворота за единицу времени; её размерность равна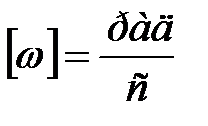 
. Угловая скорость 
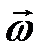– это тоже вектор, как и угловое перемещение. Он направлен так же, как и вектор , по оси вращения по правилу буравчика (рис.1.6). Запишем определение угловой скорости в векторном виде:
. (1.24а)
При равномерном вращении 
; 
. Поскольку величина линейной скорости постоянна, то касательное ускорение отсутствует 
, и полное ускорение равно центростремительному (нормальному):
.
По определению период вращения равен времени одного оборота: 
; частота (линейная частота) равна числу оборотов за единицу времени: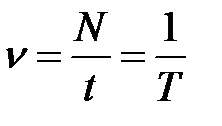 
; и можно показать, что угловая скорость равна 
.
При неравномерном вращении 
; 
. Из (1.10) и (1.23):
. (1.25)
Производная 
, показывающая быстроту изменения угловой скорости, называется угловым ускорением:
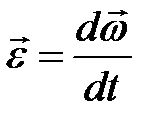. (1.26)
Угловое ускорение – это вектор, направленный также по оси вращения; его направление совпадает с направлением вектора угловой скорости 
, если скорость вращения растёт (производная положительна) и противоположно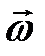 
, если происходит замедление вращения (рис.1.6).
Из (1.25) вытекает связь между линейным тангенциальным ускорением и угловым ускорением:
. (1.27)
Размерность 
.
Для произвольного вращательного движения материальной точки вокруг неподвижной оси угловое перемещение и изменение угловой скорости за время t равны соответственно (см. определения (1.24) и (1.26)):
; 
.
