Інтегральне перетворення Лапласа

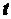    Розглянемо функцію  дійсної змінної  , яка відповідає таким умовам:

    1. При .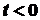

    2. При 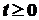 функція  на будь-якому скінченному проміжку вісі 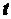 має не більше ніж скінченну кількість точок розриву першого роду.

    3. При 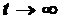 функція  має обмежену степінь зростання, тобто існують такі додатні константи  та  , що для всіх

                       .

    Інтегральне перетворення Лапласа ставить у відповідність такій функції

 функцію  комплексної змінної  за допомогою співвідношення

              .

    Функція  називається зображенням Лапласа функції  , а функція  – оригіналом функції . Зв’язок між функціями  та  будемо символічно позначати таким чином:

              .

 

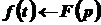Основні властивості інтегрального перетворення Лапласа.

1. Лінійність зображення                .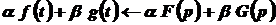

2. Теорема подібності                                                     .

3. Диференціювання оригіналу                                ;

                   .

4. Диференціювання зображення                          .

5. Інтегрування оригіналу                                                  

6. Інтегрування зображення                                             .

7. Теорема спізнення                                                     .

8. Теорема зміщення                                                        

9. Теорема множення (теорема Бореля)             .

 

Зображення Лапласа деяких функцій

 

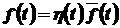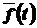    Перетворення Лапласа застосовується для функцій, які при від’ємному значенні аргумента дорівнюють нулю. Такі функції можуть бути записані у вигляді , де  – функція Хевісайда, а   – деяка функція. У подальшому будемо у більшості випадків випускати множник , маючи на увазі його наявність.

    Наведемо зображення Лапласа функцій, які найчастіше зустрічаються при розв’язуванні нескладних задач.

;                                        ;

;                                 ;

   ;                      ;

;                      .

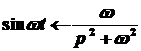    Існують спеціальні таблиці зображень елементарних та спеціальних функцій, які наведені у посібниках з інтегральних перетворень та довідниках.

    Якщо функція  є кусочно неперервною, наприклад, має вигляд  , її можна записати за допомогою функції Хевісайда у вигляді , або . Тоді відповідне зображення має вигляд . Зокрема, зображенням функції 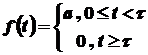 буде .