Определение числовых характеристик сл вел. Мат ожидание д.с.в. и его св-ва

Закон распределения полностью описывает ДСВ, но не всегда есть возможность его получить. В этом случае используют числа, кот описывают ДСВ суммарно, их назыв числовыми характеристиками. К ним относятся: мат ожидание, дисперсия, среднее квадратическое отклонение, начальный и центральный теоретические моменты, мода, ассиметрия и эксцесс.

пусть задан закон распределения:

x	x1	x2	…	xn
p	p1	p2	…	pn

опр: Мат ожидание ДСВ наз сумма произведений возможных значений сл вел на их вер-ти.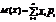

С точки зрения вер-ти мат ожидание – есть среднее арифметическое возможных значений сл вел.

Свойства математического ожидания:

1.M(C)=C, С-const.

2.M(CX)=CM(X)

3.Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M(X*Y)=M(X)*M(Y).

4.M(X+Y)=M(X)+M(Y).

Теор: Пусть производится n независимых испытаний, в каждом из которых событие А появляется с одной и той же вероятностью p, тогда математическое ожидание числа появлений события А равно: M(X)=np.

 

Дисперсия ДСВ Её свойства. Среднее квадратическое отклонение д.с.в.

Для определения возможности рассеяния возможных знач сл вел вокруг ее мат ожидания вводят понятие дисперсии.

пусть задан закон распределения:

x	x1	x2	…	xn
p	p1	p2	…	pn

опр: Дисперсией (рассеянием) случайной величины наз мат-кое ожидание квадрата отклонения сл вел от ее мат ожидания.

D(X)=M[X-M(X)]².

Дисперсия – характеристика рассеяния возм знач сл вел вокруг ее мат ожидания.

опр: Отклонением называется разность между возможными значениями случайной величины и ее математическим ожиданием. [X-M(X)] – отклонение.

Свойтсва:

1.D(C)=0

2.D(СХ)=СD(Х)

3.Х,У- независ, D(X+Y)=D(X)+D(Y)

4.Х,У- независ, D(X-Y)=D(X)+D(Y)

5.Пусть соб А в n независимых испытаниях, в каждом из кот соб А появится с 1й и той же вер-тью p и не появиться с вер-тью q, тогда дисперсия числа появлений соб А D(X)=npq

Для вычислений удобна формула: D(X)=M(X²)-[M(X)]²

Еще одной хар-кой рассеяния возм знач сл вел вокруг ее мат ожидания явл-ся среднее квадратическое отклонение(СКО)

опр: Средним квадратическим отклонением s(х) наз корень из дисперсии..

СКО применяется тогда, когда размерность результата должна совпадать с размерностью сл вел-ы.

 

Начальные и центральные теоретич моменты ДСВ. Мода. Асимметрия. Эксцесс.

опр: Начальным теоретическим моментом порядка k случайной величины X называется мат ожидание сл вел в k -й степени. n_k=M(X^k).

Частный случай: n₁=M(X); n₂=M(X²); Следовательно, D=n₂-(n₁)²_.

опр: Центральным теоретическим моментом порядка k сл вел Х назыв мат ожидание от отклонения сл вел в k -й степени. m_k=M(X-M(X))^k.

Частный случай: m₁=M(X-M(X))=0 (по основному свойству отклонения);

m₂=М((X-M(X))²)=D(X).

m₂=n₂-(n₁)² – связь м/у начальным и центральным моментами.

m₃=n₃-3n₂n₁+2(n₁)³; m₄=n₄-4n₃n₁+6n₂(n₁)²-3(n₁)⁴;

опр: Модой случайной величины Х называется наиболее вероятное ее значение М₀(Х). Данное определение справедливо только для ДСВ.

опр: Ассиметрией сл вел Х наз отношение центрального теоретического момента 3-го порядка к кубу среднего квадратического отклонения. As=m₃/s³;

опр: Эксцессом случайной величины Х называется величина равная E_k=(m₄/s⁴)-3;