Имеется большое число задач, в которых вычисление вероятностей выполняется с помощью комбинаторных формул. Рассмотрим основные комбинаторные формулы.
19.1. Перестановки. Пусть имеется 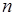 различных объектов
различных объектов 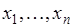 . Эти объекты перенумерованы, и следовательно, образуют последовательность (или упорядоченное множество). Поменяем местами два объекта
. Эти объекты перенумерованы, и следовательно, образуют последовательность (или упорядоченное множество). Поменяем местами два объекта 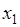 и
и 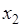 . Тогда получим новую последовательность
. Тогда получим новую последовательность 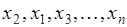 . Затем можно в исходной последовательности на первое место поставить
. Затем можно в исходной последовательности на первое место поставить 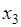 , а объект
, а объект 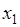 соответственно на третье и т.д., получая каждый раз новую последовательность из
соответственно на третье и т.д., получая каждый раз новую последовательность из 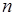 объектов. Разные последовательности отличаются только порядком следования объектов, поэтому в общем случае последовательность, полученная при перестановке объектов, имеет вид:
объектов. Разные последовательности отличаются только порядком следования объектов, поэтому в общем случае последовательность, полученная при перестановке объектов, имеет вид: 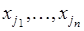 .
.
Возникает вопрос, чему равно число разных последовательностей 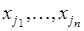 ? (Или просто чему равно число перестановок?) Ответ может быть получен путем следующих рассуждений. Объект
? (Или просто чему равно число перестановок?) Ответ может быть получен путем следующих рассуждений. Объект 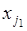 можно выбрать
можно выбрать 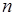 способами, то есть в качестве
способами, то есть в качестве 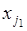 можно взять любой объект среди
можно взять любой объект среди 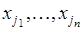 . Если
. Если 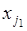 выбран, то
выбран, то 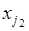 можно выбрать
можно выбрать 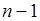 способом, поскольку в исходной последовательности осталось
способом, поскольку в исходной последовательности осталось 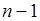 объектов, каждый из которых может быть выбран в качестве второго объекта
объектов, каждый из которых может быть выбран в качестве второго объекта 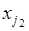 новой последовательности и т.д. Всего, таким образом, существует
новой последовательности и т.д. Всего, таким образом, существует 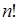 способов образовать последовательность
способов образовать последовательность 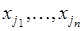 , выбирая объекты из совокупности
, выбирая объекты из совокупности 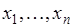 . Число
. Число 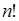 называется числом перестановок
называется числом перестановок 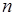 разных объектов.
разных объектов.
19.2. Размещения. Усложним условие задачи. Пусть имеется 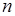 различных объектов
различных объектов 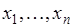 . Чему равно число разных последовательностей вида
. Чему равно число разных последовательностей вида 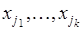 ,
, 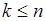 , полученных при извлечении
, полученных при извлечении 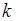 объектов из исходной последовательности
объектов из исходной последовательности 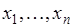
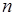 разных объектов?
разных объектов?
Аналогично как и в первой задаче, в данном случае объект 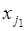 можно выбрать
можно выбрать 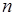 способами. Если
способами. Если 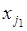 выбран, то объект
выбран, то объект 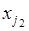 можно выбрать
можно выбрать 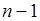 способом и т.д. Наконец, объект
способом и т.д. Наконец, объект 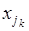 можно выбрать
можно выбрать 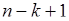 способом. Таким образом, всего существует
способом. Таким образом, всего существует
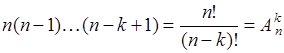 (19.1)
(19.1)
способов образовать последовательность из 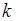 объектов, выбирая объекты из совокупности
объектов, выбирая объекты из совокупности 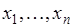 . Иначе эту задачу можно сформулировать следующим образом: сколько существует способов размещения
. Иначе эту задачу можно сформулировать следующим образом: сколько существует способов размещения 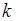 из
из 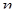 различных объектов по
различных объектов по 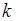 местам. Число
местам. Число 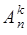 (19.1) называется числом размещений из
(19.1) называется числом размещений из 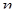 по
по 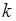 . Отметим, что при
. Отметим, что при 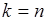 из (19.1) следует
из (19.1) следует 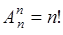 .
.
19.3. Сочетания. Пусть имеется 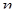 различных объектов
различных объектов 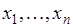 , из которых выбирается
, из которых выбирается 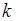 объектов
объектов 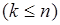 , образующих множество
, образующих множество 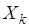 . Сколькими способами можно образовать множество
. Сколькими способами можно образовать множество 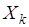 ?
?
В отличие от размещений результатом извлечений объектов из совокупности 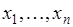 является не последовательность, а множество
является не последовательность, а множество 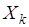 . В последовательности важен порядок расположения элементов, так две последовательности
. В последовательности важен порядок расположения элементов, так две последовательности 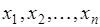 и
и 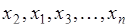 — разные, они различаются расположением элементов
— разные, они различаются расположением элементов 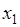 и
и 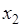 . Если рассматривать два множества
. Если рассматривать два множества 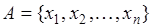 и
и 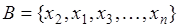 , то эти множества одинаковые:
, то эти множества одинаковые: 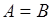 , поскольку порядок расположения элементов
, поскольку порядок расположения элементов 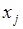 на множестве не имеет значения. Важен только вопрос: содержится элемент
на множестве не имеет значения. Важен только вопрос: содержится элемент 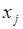 в данном множестве или нет? Таким образом, данная задача отличается от задачи на число размещений тем, что извлекаемые
в данном множестве или нет? Таким образом, данная задача отличается от задачи на число размещений тем, что извлекаемые 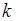 объектов образуют множество
объектов образуют множество 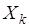 , на котором не важен порядок расположения объектов, а важен только факт наличия или отсутствия элемента
, на котором не важен порядок расположения объектов, а важен только факт наличия или отсутствия элемента 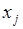 в множестве
в множестве 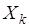 .
.
Сочетанием из 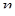 элементов по
элементов по 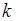 называется любое подмножество из
называется любое подмножество из 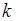 элементов множества, содержащего
элементов множества, содержащего 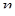 элементов. Число всех сочетаний обозначается записью
элементов. Число всех сочетаний обозначается записью 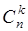 . Наша задача сводится к нахождению числа
. Наша задача сводится к нахождению числа 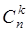 . Если, извлекая объекты из совокупности
. Если, извлекая объекты из совокупности 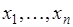 , строить из них последовательность
, строить из них последовательность 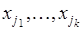 , то есть учитывая расположение объектов, то число разных последовательностей равно числу
, то есть учитывая расположение объектов, то число разных последовательностей равно числу 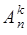 - размещений из
- размещений из 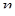 по
по 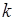 . В данной задаче интерес представляет множество
. В данной задаче интерес представляет множество 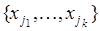 , для которого разный порядок расположения
, для которого разный порядок расположения 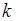 заданных элементов
заданных элементов 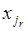 дает одно и то же множество. Число перестановок
дает одно и то же множество. Число перестановок 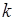 разных элементов равно
разных элементов равно 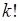 . Поэтому число размещений
. Поэтому число размещений 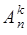 в
в 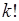 больше числа сочетаний
больше числа сочетаний 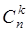 . Из (19.1) следует
. Из (19.1) следует
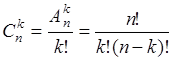 (19.2)
(19.2)
19.4. Перестановки с повторениями. Имеется 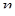 объектов, но не все эти объекты разные, среди них имеются одинаковые объекты или неразличимые. Пусть среди
объектов, но не все эти объекты разные, среди них имеются одинаковые объекты или неразличимые. Пусть среди 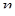 объектов
объектов 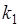 объектов 1-го типа,
объектов 1-го типа, 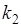 объектов 2-го типа, …,
объектов 2-го типа, …, 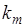 объектов
объектов 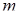 -го типа. Других объектов нет, так что
-го типа. Других объектов нет, так что
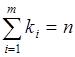 . (19.3)
. (19.3)
Чему равно число 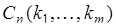 разных последовательностей из
разных последовательностей из 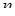 объектов, которые можно образовать, извлекая их из совокупности в
объектов, которые можно образовать, извлекая их из совокупности в 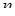 объектов?
объектов?
Если все 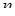 объектов были бы разными, например пронумерованы от 1 до
объектов были бы разными, например пронумерованы от 1 до 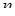 , то число разных последовательностей было бы равно
, то число разных последовательностей было бы равно 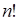 . Поскольку имеются
. Поскольку имеются 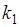 неразличимых объектов 1-го типа, то перестановка двух объектов 1-го типа между собой не дает новой последовательности. Это следует учесть. Число перестановок между объектами 1-го типа равно
неразличимых объектов 1-го типа, то перестановка двух объектов 1-го типа между собой не дает новой последовательности. Это следует учесть. Число перестановок между объектами 1-го типа равно 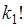 Поэтому за счет неразличимости перестановок между объектами 1-го типа, общее число разных последовательностей уменьшается в
Поэтому за счет неразличимости перестановок между объектами 1-го типа, общее число разных последовательностей уменьшается в 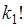 раз. Аналогично следует учесть неразличимые перестановки между объектами 2-го типа, их
раз. Аналогично следует учесть неразличимые перестановки между объектами 2-го типа, их 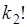 и т.д. Таким образом, число
и т.д. Таким образом, число 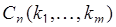 разных перестановок совокупности из
разных перестановок совокупности из 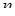 объектов, среди которых
объектов, среди которых 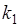 объектов 1-го типа,
объектов 1-го типа, 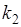 объектов 2-ого типа, …,
объектов 2-ого типа, …, 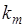 объектов
объектов 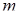 -го типа, равно
-го типа, равно
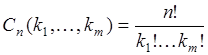 . (19.4)
. (19.4)
Из (19.4) следует при 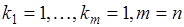 , то есть при условии что все объекты разные,
, то есть при условии что все объекты разные,
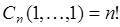 (19.5)
(19.5)
- число перестановок 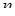 разных объектов (или без повторения).
разных объектов (или без повторения).
Из (19.4) можно получить другой частный случай при 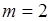 ,
, 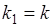 ,
, 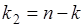 :
:
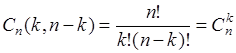 , (19.6)
, (19.6)
что позволяет интерпретировать 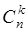 как число перестановок
как число перестановок 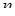 объектов, среди которых
объектов, среди которых 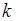 объектов 1-го типа и
объектов 1-го типа и 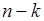 объектов 2-го типа.
объектов 2-го типа.
19.5. Размещения с повторениями. Пусть имеется 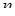 разных объектов
разных объектов 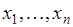 , из которых выбирается объект, фиксируется и возвращается обратно. Таким образом извлекается
, из которых выбирается объект, фиксируется и возвращается обратно. Таким образом извлекается 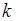 объектов
объектов
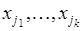 . (19.7)
. (19.7)
Последовательность (19.7) называется размещением с повторениями из 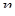 (элементов) по
(элементов) по 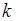 (местам). Таким образом, в последовательности (19.7) могут встречаться одинаковые объекты, в отличие от размещения (без повторения), когда объекты извлекаются из исходной совокупности без возвращения.
(местам). Таким образом, в последовательности (19.7) могут встречаться одинаковые объекты, в отличие от размещения (без повторения), когда объекты извлекаются из исходной совокупности без возвращения.
Сколькими способами может быть образована последовательность (19.7) при извлечении с возвращением? Поскольку первый объект 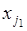 может быть выбран
может быть выбран 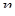 способами, второй объект
способами, второй объект 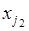 -также
-также 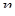 способами и т.д., то существует
способами и т.д., то существует
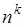 (19.8)
(19.8)
размещений из 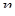 по
по 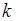 с повторениями.
с повторениями.
 2020-01-15
2020-01-15 117
117








