Показатель эффективности моделируемой системы – вероятность появления некоторого случайного события

 

В каждой из N реализаций имитационного эксперимента некоторое событие А может наступить с вероятностью p и не наступить с вероятностью 1-p. В этом случае оценкой показателя эффективности является относительная частота наступления события А

,

где m – число случаев, в которых событие наступило.

На основания выражения (1) получаем выражение:

       (2)

m – дискретная случайная величина, определяемая следующим образом:

В соответствии с центральной предельной теоремой, относительная частота наступления события имеет распределение, близкое к нормальному, тогда величина y=  также может рассматриваться как нормальная случайная величина.

 

Дальнейший вывод продолжим с использованием интеграла вероятностей:

 

0,5

t

u

Ф

Корнем уравнения Ф(U)=  является  – квантиль нормального распределения.

Ф(-U)=1-Ф(U)

Нормируем соотношение (2):

U =  ~ Norm(0,1), т.е. величина U имеет нормированное нормальное распределение.

                            (3)

Если вероятность p имеет меньший порядок, чем абсолютная точность , применяется относительная точность 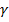 =  и выражение (3) преобразуется в (4):

.                      (4)