Інваріантне означення ротора

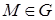Нехай в області визначено векторне поле . Зафіксуємо точку і деяку площину, яка проходить через цю точку. Нехай – одиничний вектор нормалі до площини, – замкнений контур, який лежить в площині і обмежує область таку, що 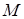– внутрішня точка області . Запишемо формулу (12) для векторного поля в області . Застосовуючи до правої частини цієї формули теорему про середнє, отримуємо

диференціальне векторне поле формула соленоїдальне

звідки

де – площа області , – деяка точка області .

Стягуватимемо область до точки так, щоб залишалася внутрішньою точкою області . Тоді , а прямуватимемо до . Внаслідок неперервності значення 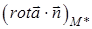прямуватимемо до . Таким чином, отримуємо

У праву частину формули входять величини, інваріантні відносно вибору системи координат (циркуляція векторного поля вздовж замкненого контура і площа плоскої області). Тому дана формула дає інваріантне означення проекції 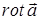в точці на напрям, який виражається заданим вектором .

Отже, проекція ротора векторного поля на довільний напрям, а отже, і сам 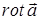залежить тільки від векторного поля і не залежить від вибору системи координат.

Для означення вектора вищезазначеним способом достатньо розглянути в заданій точці проекції на три довільних некомпланарних напрями. Такими трьома проекціями визначається однозначно.