Силовой расчет ведущего звена

Рассмотрим равновесие звена АВ. К нему приложены следующие силы (рис. 4.21): в точке В – сила 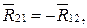 в точке А – вес зубчатого колеса  и реакция  в точке – вес кривошипа  и центробежная сила инерции

Уравнение равновесия ведущего звена:

                      .            (4.37)

Силу  находим из уравнения моментов сил, приложенных к звену 1, относительно точки А.

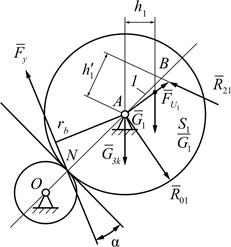
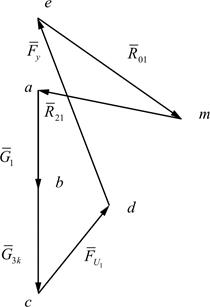
Рис. 4.21. Первоначальный механизм	Рис. 4.22. План сил ведущего звена

Плечом уравновешивающей силы будет радиус основной окружности  зубчатого колеса:

                                            ,                                  (4.38)

                                                       (4.39)

¨ откуда

                                                           (4.40)

После определения величины  построением замкнутого многоугольника сил согласно уравнению (4.37) определяется реакция стойки на звено 1  (рис. 4.22):

4.9.5. Определение уравновешивающей силы (F_y)
с помощью рычага Жуковского

Поворачиваем план скоростей для рассматриваемого положения механизма на 90° по направлению, противоположному вращению часовой стрелки. Все внешние силы, включая и силы инерции звеньев, переносим параллельно самим себе в соответствующие точки плана (рис. 4.23).

Скорость точки приложения уравновешивающей силы

.

Далее составляем уравнение равновесия рычага Жуковского в следующем виде:

При наличии моментов  приложенных к звеньям, можно обойтись и без замены их парой сил. В этом случае к плану скоростей прикладываются моменты  определяемые по уравнениям:

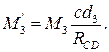
Рис. 4.23. Повернутый план скоростей

 

При этом момент 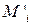 имеет тот же знак, что и момент , если CD на плане механизма и  на повернутом плане скоростей совпадают по направлению. Если направление  противоположно CD,то моменты  и 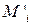 имеют разные знаки.

Таким образом, если к звеньям механизма приложены силы и моменты, то уравнение равновесия вспомогательного рычага можно написать в следующем виде:

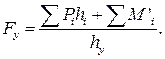
Мощность двигателя определяется по аналогии с предыдущим примером.

4.10. Принцип виртуальных перемещений
для силового расчёта

Запишем для механизма принцип виртуальных перемещений в координатной форме:

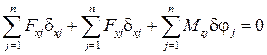                           ,                (4.41)

где – проекции всех сил, приложенных к звеньям механизма, кроме реакций в кинематических парах; – моменты всех сил, приложенных к звеньям; – виртуальные осевые перемещения точек приложения сил; – виртуальные угловые перемещения звеньев механизма; n – число сил и моментов сил. Это уравнение является основным для силового расчета. Из него получаем два вывода:

1. Для равновесия механизма в целом и в каждой его точке нельзя задавать произвольно все внешние силы, часть из них должна быть определена в процессе расчета. Такие силы называют уравновешивающими силами , их число равно числу обобщенных координат механизма. Часто определяют не уравновешивающие силы, а уравновешивающие моменты , так как они связаны с уравновешивающими силами простыми соотношениями.

Рассмотрим механизм строгального станка с приложенной к резцу силой полезного сопротивления  (рис. 4.24). Какую силу необходимо приложить в точке  перпендикулярно звену , чтобы механизм находился в равновесии? Применяем принцип виртуальных перемещений:

                                       .                             (4.42)

Из планов виртуальных перемещений, построенных на схеме механизма, выразим перемещение  через :

                                    (4.43)

.

Подставляя в (4.42), получим:

                           (4.44)

Рис. 4.24. Определение уравновешивающей силы F_y
из принципа виртуальных перемещений

 

Уравновешивающий момент найдем из соотношения:

                                                                              (4.45)

Именно этот момент надо приложить со стороны двигателя (извне), чтобы преодолеть силу полезного сопротивления. В теории механизмов принцип виртуальных перемещений редко используют непосредственно, а учитывают, что при голономных стационарных связях виртуальные перемещения совпадают с действительными перемещениями, поэтому:

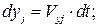
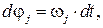                                   (4.46)

где 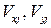– проекции скоростей точек приложения сил; – угловые скорости звеньев.

Сокращая затем на dt, получают с учетом (4.41):

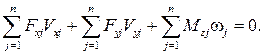                                              (4.47)

Для механизмов с одной обобщенной координатой уравновешивающий момент находим из выражения:

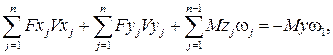                                (4.48)

¨ где – обобщенная угловая скорость.

Окончательно получим:

                          (4.49)

2. Из принципа виртуальных перемещений легко получают условия равновесия плоской системы сил. Так как в уравнении (4.41) виртуальные перемещения являются независимыми, то для равенства нулю левой части необходимо:

                                                            (4.50)

Такие уравнения можно составлять как для всего механизма, так и для отдельных его звеньев. В этом случае реакции связей относят к категории внешних сил. В ТММ принято вести силовой расчет погруппно, т.к. группы Ассура являются статически определимыми.