2020-01-14
143
Для данного положения механизма (рис. 4.8) произвести кинетостатический расчет, т.е. определить давления (реакции) во всех кинематических парах и потребную мощность двигателя.
Считаем известными размеры звеньев, положения центров тяжести, веса, момент инерции звеньев относительно собственных центров тяжести Jsi,силу полезного сопротивления Fnc и угловую скорость кривошипа ω= const. Главный вал рабочей машины соединен с ведущим валом посредством муфты.
4.8.1. Определение сил инерции звеньев
и моментов пары сил
В общем случае плоскопараллельного движения все силы инерции каждого звена могут быть приведены к главному вектору сил инерции, приложенному в центре масс звена, и к паре сил инерции. Величина силы инерции определяется как произведение массы звена на ускорение центра тяжести:
, H,
и направлена эта сила в сторону, противоположную ускорению центра тяжести. Ускорение центра тяжести берется из плана ускорений для рассматриваемого положения механизма (см. рис. 4.8):
Н, (4.1)
Н, (4.2)
Н, (4.3)
Н, (4.4)
Н, (4.5)
¨ где g – ускорение земного притяжения (
).
Момент пары сил инерции равен произведению момента инерции Jsi звена относительно оси, проходящей через центр тяжести, на угловое ускорение звена:
(4.6)
Направление действия момента пары сил инерции противоположно угловому ускорению звена. Угловое ускорение каждого звена определяется как частное от деления относительного тангенциального ускорения каких-либо двух его точек на расстоянии между точками: 
, так как ω1 = const и, следовательно, ε1= 0;
, Hм, (4.7)
, Hм, (4.8)
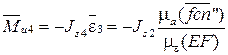, Нм, (4.9)
= 0, так как звено 5 движется поступательно.
Рис. 4.8. Схема механизма: а – план положения механизма;
б – план скоростей; в – план ускорений
Для определения направления углового ускорения второго звена переносим с плана ускорений отрезок сп, изображающий тангенциальное ускорение точки С звена СВ относительно точки 5, в точку С механизма.
Вектор 
,приложенный в точке С, производит вращение звена ВС относительно точки В против направления вращения часовой стрелки. Следовательно, таким и будет направление углового ускорения 
.
Направление действия момента Ми пары сил инерции будет противоположно угловому ускорению . Направление углового ускорения 
звена 3 определяется по тангенциальному ускорению . Для этого достаточно вектор 
мысленно приложить в точке С механизма и проверить, каково будет направление вращения звена CD относительно точки D.
На рис. 4.8, а это направление совпадает с направлением вращения часовой стрелки. Значит, момент 
будет направлен против направления вращения часовой стрелки.
Аналогично определяется направление углового ускорения (см. рис. 4.8, а). Угловое ускорение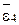 
направлено против направления вращения часовой стрелки, а момент 
действует по направлению вращения часовой стрелки.
4.8.2. Определение реакций в кинематических парах
структурной группы 2 класса 2-го вида (звенья 5 и 4)
Разбиваем механизм на группы Ассура и начинаем рассмотрение с той группы, для которой известны все внешние силы. Порядок рассмотрения групп при кинетостатическом расчете будет обратным порядку кинематического.
Скорость точки приложения уравновешивающей силы:
Далее составляем уравнение равновесия рычага Жуковского в следующем виде:
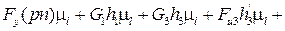
, (4.10)
(4.11)
Таким образом, если к звеньям механизма приложены силы и моменты, то уравнение равновесия вспомогательного рычага можно написать в следующем виде:
. (4.12)
Мощность двигателя определяется по аналогии с предыдущим примером.
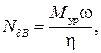
где η –КПД механизма исследования. Поэтому в первую очередь рассматриваем структурную группу 22, состоящую из звеньев 4 – 5. Эта структурная группа со всеми действующими на нее силами, включая и силы инерции, показана на рис. 4.9.
Действие отброшенных звеньев заменено действием реакций 
и 
, которые необходимо определить. Разложим реакцию 
на две составляющие: 
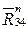– реакция, действующая вдоль звена EF, 
– действующая перпендикулярно звену EF, при этом
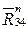= + . (4.13)
Рис. 4.9. Структурная группа 
Реакция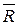 
05 будет проходить через центр шарнира F,так, все силы, действующие на звено 5, проходят через центр шарнира F.
За порядком нахождения искомых реакций (давлений) в структурной группе 22 можно проследить по табл. 4.1.
Таблица 4.1
Таблица для определения реакций в кинематических парах
| Искомый параметр | Уравнения равновесия | Звено, для которого составляется уравнение |
| 
| 4 |
 05 и 05
| 
| 4 и 5 |
|
| 5 |
Далее приступаем к написанию развернутых уравнений равновесия и к определению сил.
1. Величина может быть непосредственно получена из уравнения равновесия, написанного для звена 4.
Звено 4 находится под действием следующих сил: веса G4,результирующей силы инерции Fu 4, составляющих 
и 
реакции 
и реакции 
,которой заменено действие отсоединенного звена 5.
Направление силы 
определяется составлением уравнения моментов всех сил, действующих на звено 4 относительно точки F.
Если величина силы окажется отрицательной, то направление должно быть выбрано противоположным.
, (4.14)
¨ откуда
(4.15)
2. Составляем уравнение равновесия структурной группы, приравнивая к нулю векторную сумму всех сил, действующих на группу
. (4.16)
При составлении векторной суммы сил удобно неизвестные по величине силы писать в начале и в конце уравнения, чтобы при построении плана сил было проще найти их величину.
Кроме того, при составлении уравнения (4.16) рационально силы, относящиеся к одному звену, писать последовательно друг за другом, так как это упрощает в дальнейшем определение реакции во внутренней кинематической паре.
Построение плана сил для структурной группы 
показано на рис. 4.10.
Если наибольшая сила Fnc, то
¨ где 
– вектор силы Fnc на плане сил (4.17).
Рис. 4.10. План сил структурной группы
Далее в этом масштабе из точки а проводим линию действия нормальной составляющей реакции звена 3 на звено 4 и откладываем отрезок |bc|,выражающий в масштабе μ F силу .
Затем к концу вектора прибавляем вектор G 4и так далее согласно уравнению (4.16).
Из конца вектора 
проводим линию действия реакции 
05. Точка а – точка пересечения линий действия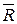 
05и .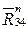
Геометрически сложив 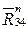и , определим полную реакцию в шарнире Е.
Отрезок 
изображает искомую реакцию 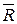05:
а отрезок 
– искомую реакцию 
:
3. Реакция во внутренней кинематической паре определяется из условия равновесия звена 5:
(4.17)
Реакция R 45 неизвестна ни по величине, ни по направлению.
Так как при построении плана сил для структурной группы 
были сгруппированы силы по звеньям, то нового плана сил для звена 5 строить не требуется. Достаточно соединить конец силы R 05(точка а)с началом силы G 5(точка В), чтобы получить реакцию R 45.
Для равновесия звена 4 надо замкнуть многоугольник сил, действующих на звено 4, т.е. соединить конец вектора 
(точка m) с началом вектора 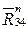(точка а).
Иными словами: 
= – 
4.8.3. Определение реакций в кинематических парах
структурной группы 2
Рассмотрев диаду 4 – 5, переходим к следующей структурной группе 2 класса 1-го вида, состоящей из звеньев 2 и 3 (рис. 4.11). При этом определенную нами реакцию  поворачиваем на 180°, получаем реакцию  и прикладываем ее в точке Е звена 3 как известную внешнюю силу.
Порядок определения реакций в кинематических парах структурной группы  указан в табл. 4.2, а соответствующие планы сил даны на рис. 4.12.
| 
Рис. 4.11. Структурная группа 
|
1. Сумма моментов всех сил, действующих на звено 2, относительно точки С:
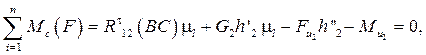
¨ откуда
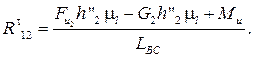
2. Сумма моментов всех сил, действующих на звено 3 относительно точки С:
(4.18)
¨ откуда
(4.19)
Рис. 4.12. План сил структурной группы 
Таблица 4.2
Таблица для определения реакций в кинематических парах
 Искомый параметр
| Уравнение равновесия | Звено, для которого составляется уравнение |
| 
| 2 |
|
| 3 |
 и 
| 
| 2 и 3 |
|
| 2 |
3. Общее уравнение равновесия всей структурной группы (см. рис. 4.11)
(4.20)
Построение начинаем в точке а, в которой заканчивается вектор 
и из которой исходит 
.
Очевидно, что
, (4.21)
(4.22)
Отрезок 
на плане сил (см. рис. 4.12) в масштабе 
изображает реакцию 
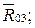отрезок 
– реакцию 
,
.
4. Для определения силы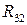 
составляем уравнение равновесия звена 2:
(4.23)
Соединив конец вектора 
(точка а) с началом вектора 
(точка b), получим в масштабе 
величину силы 
и ее направление (см. линию 
на рис. 4.12).
; 
и может быть найдена из уравнения равновесия звена 3.
