Определяем силы инерции звеньев и точки их приложения, для этого разбиваем механизм на структурные группы Ассура, так как они статически определимы.
Звенья 5 и 4 образуют структурную группу 2-го класса, 5-го вида, 2-го порядка.
Звенья 2 и 3 образуют структурную группу 2-го класса, 3-го вида, 2-го порядка.
Звено I, соединенное вращательной кинематической парой со стойкой, представляет начальный механизм 1-го класса.
Структурная формула строгального станка: 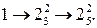
4.9.2. Определение реакций в кинематических парах
структурной группы 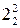 (звенья 5 и 4)
(звенья 5 и 4)
Силовой расчет начинаем с наиболее удаленной структурной группы, состоящей из звеньев 4–5 (рис. 4.17), так как все внешние силы, действующие на эту структурную группу, известны. Действие отброшенных звеньев заменено действием реакции 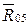 и
и 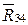 . Сила
. Сила 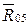 действует по нормали к
действует по нормали к 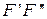 , но точка приложения этой силы неизвестна. Сила
, но точка приложения этой силы неизвестна. Сила 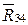 приложена к точке D, но линия действия ее неизвестна.
приложена к точке D, но линия действия ее неизвестна.
Порядок определения реакций приведен в табл. 4.3.
1. Из условия равновесия звена 5 имеем
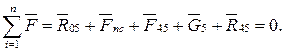 (4.27)
(4.27)
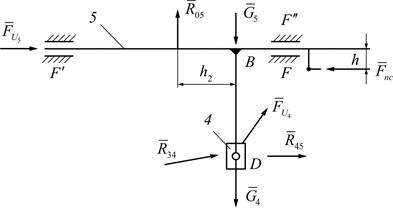
Рис. 4.17. Структурная группа 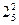
Реакция звена 4 на звено 5 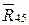 перпендикулярна направляющей и проходит через точку D.
перпендикулярна направляющей и проходит через точку D.
Таблица 4.3
Таблица для определения реакций в кинематических парах
| Искомый параметр | Уравнение равновесия | Звено, для которого составляется уравнение |
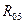 и и 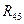
| 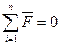
| 5 |
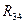
| 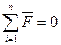
| 4 |
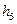
| 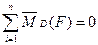
| 5 |
Построение начинаем с точки m (рис. 4.18), откладывая силу Fnc, и последовательно к ней присоединяем все силы, действующие на звенья механизма в масштабе μ f.
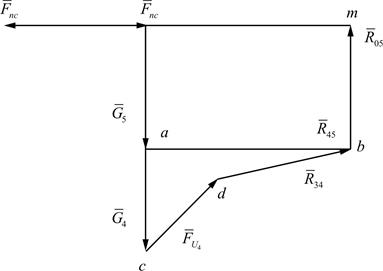
Рис. 4.18. План сил структурной группы 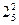
Пересечение линий действия векторов 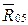 и
и 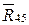 даст тоску b, которая ограничит эти векторы по величине:
даст тоску b, которая ограничит эти векторы по величине:
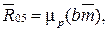
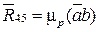 .
.
2. Сила 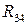 найдется из условия равновесия звена 4.
найдется из условия равновесия звена 4.
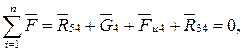 (4.28)
(4.28)
очевидно, 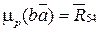 (см. рис. 4.18)
(см. рис. 4.18)
Следовательно, в этом уравнении неизвестна только одна сила 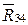 , которая легко может быть определена построением силового многоугольника bacdb (см. рис. 4.18):
, которая легко может быть определена построением силового многоугольника bacdb (см. рис. 4.18):
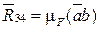 .
.
3. Для определения плеча 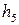 силы
силы 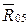 составляем уравнение моментов всех сил, действующих на звено 5 относительно точки D (см. рис. 4.18):
составляем уравнение моментов всех сил, действующих на звено 5 относительно точки D (см. рис. 4.18):
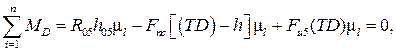 (4.29)
(4.29)
¨ откуда
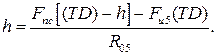 (4.30)
(4.30)
4.9.3. Определение реакций в кинематических парах
структурной группы 23 (звенья 3 и 2)
Прикладываем к точке D силу 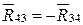 .
.
1. Звенья 1 и 2 соединены вращательной кинематической парой, следовательно, реакция 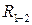 приложена в шарнире B. Звенья 2 и 3 образуют поступательную кинематическую пару, следовательно, реакция между ними направлена перпендикулярно к BC. Так как на звено 2 действуют только две силы-реакции (
приложена в шарнире B. Звенья 2 и 3 образуют поступательную кинематическую пару, следовательно, реакция между ними направлена перпендикулярно к BC. Так как на звено 2 действуют только две силы-реакции (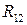 и
и 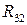 ),
), 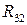 тоже пройдет через точку B (рис. 4.19).
тоже пройдет через точку B (рис. 4.19).
Порядок определения реакций в кинематических парах структурной группы 23приведен в табл. 4.4, а соответствующие планы сил на рис. 4.20.
Сумма моментов всех сил диады относительно точки С:
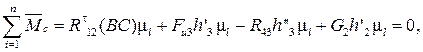 (4.31)
(4.31)
¨  откуда
откуда
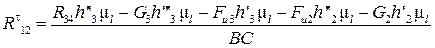 . (4.32)
. (4.32)
2. Из равновесия звена 2 имеем
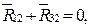 (4.33)
(4.33)
¨ так как 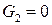 ,
,
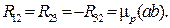 (4.34)
(4.34)
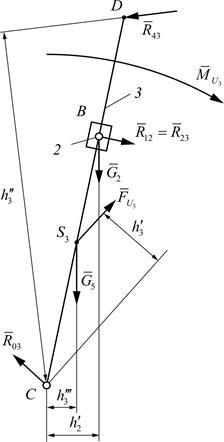 Рис. 4.19. Структурная группа
Рис. 4.19. Структурная группа 
|
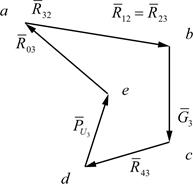 Рис. 4.20. План сил структурной группы
Рис. 4.20. План сил структурной группы 
|
Таблица 4.4
Таблица для определения реакций в кинематических парах
| Искомый параметр | Уравнение равновесия | Звено, для которого составляется уравнение |
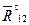
| 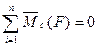
| 2 и 3 |
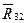
| 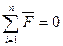
| 2 |
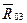
| 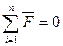
| 3 |
3. Из уравнения равновесия звена 3 находим 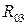 , помня, что
, помня, что 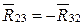 .
.
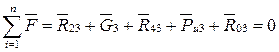 (4.35)
(4.35)
¨ (см. силовой замкнутый многоугольник abcde на рис. 4.20)
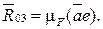 (4.36)
(4.36)
 2020-01-14
2020-01-14 121
121








