2020-01-14
214
Количественный анализ кинетических закономерностей топохимических реакций, том числе реакций диссоциации, очень сложен. Однако, рассмотрев несколько идеализированных случаев диссоциации, можно выяснить влияние ряда факторов на кинетику рассматриваемого процесса. Для реакций твердого тела с газообразным реагентом получили распространение относительно простые выражения, отражающие те или иные особенности реакции на различных этапах ее протекания.
Одним из этих выражений является уравнение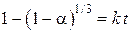 
, соответствующее модели сжимающегося (уменьшающегося) объема исходной фазы. В ней предполагается быстрое и сплошное зародышеобразование и последующее увеличение границы раздела и продвижение ее в объем старой фазы. Эта модель применяется также для описания кинетики реакции на заключительном этапе (после максимума скорости реакции) при отсутствии диффузионных торможений в слое твердых продуктов.
Кинетика процесса, протекающего в диффузионном режиме, может быть описана уравнением 
.
Нередко при анализе кинетики диссоциации применяют уравнение Ерофеева – Колмогорова в виде 
или чаще в логарифмической форме
.
Если процесс не лимитируется сложной в кинетическом описании кристаллохимической стадией зарождения новой фазы, то обратимую реакцию диссоциации - образования карбоната можно представить схемой
Скорость ее равна:
,
где 
и 
– константы скорости прямой и обратной реакций.
Уравнение можно записать в виде:
.
Для равновесия 
и 
. Тогда из равенства
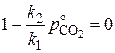
следует, что
и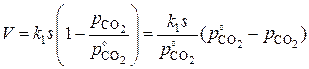 
.
Приняв
,
получим
. (1)
Полученное уравнение показывает, что скорость процесса определяется величиной реакционной поверхностью, температурой и степенью химического пересыщения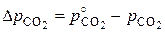 
.
Если исходное соединение состоит из частиц сферической формы с начальным радиусом 
и имеет массу 
, то к моменту времени t произойдет изменение массы 
и радиуса 
, где m и r – масса материала и радиус частиц к моменту времени t. Тогда степень превращения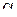 
исходного вещества 
. Для каждой из частиц 
, где 
– плотность вещества. Подставляя m и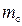 
в выражение для 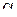, получаем
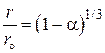(2)
Скорость процесса V, выраженная через изменение количества (моль) исходного вещества в единицу времени
(3)
где M – молярная масса вещества.
Сравнивая полученное выражение с уравнением (1) для скорости процесса в кинетическом режиме и учитывая в последнем 
, получим
и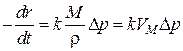 
.
При постоянных значениях температуры (
), давления 
и молярного объема 
скорость уменьшения размера непрореагировавшей части исходного соединения постоянна, то есть линейная скорость 
. После интегрирования этого уравнения от 0 до t и от r o до r получаем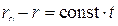 
. Отсюда относительная толщина слоя продукта
.
Записав отношение размера непрореагировавшей части исходного соединения к начальному размеру через степень превращения, приходим к уравнению
.
Это уравнение, приведенное к форме
,
известно как закономерность модели сжимающегося объема или как уравнение Мак-Кевана. Оно предполагает быстрое образование границы раздела фаз с последующим линейным во времени продвижением реакционной зоны в объем разлагающегося кристалла.
Для полного завершения диссоциации (
) требуется время
(4)
Оно, как видно, уменьшается с уменьшением размера частиц материала, с ростом температуры (что соответствует увеличению константы скорости), с уменьшением фактического парциального давления газа в реакторе (что соответствует увеличению 
).
Если в процессе диссоциации продукт оказывается малопористым, плотным, то имеются значительные диффузионные торможения, и процесс может осуществляться в диффузионном режиме. Адсорбционно–кристаллохимические реакции идут быстро, и поэтому в порах на границе раздела фаз устанавливается давление, близкое к равновесному 
, и соответствующая ему концентрация газа 
. На наружной поверхности частично прореагировавшего зерна устанавливается концентрация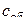 
, соответствующая давлению 
в объеме газа при отсутствии внешнедиффузионных торможений.
Скорость диффузии газа через слой оксида в соответствии с законом Фика
,
где D – коэффициент диффузии газа.
Для процесса со сферической формой частиц
(5)
где 
– радиус сферы в слое оксида, изменяющийся от r o до r за время t.
При решении этого уравнения возможны несколько различных допущений. В первом приближении для квазистационарного процесса градиент концентрации 
может быть заменен отношением приращений 
. Тогда
.
Введя в данное выражение скорость из выражения (3)
,
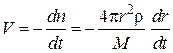получим
(6)
Отсюда следует, что линейная скорость обратно пропорциональна толщине оксидного слоя. Разделим переменные и проинтегрируем
.
Тогда
,
то есть толщина слоя продукта изменяется во времени по параболическому закону 
. Введя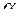 
из уравнения 
(2), получим выражение
,
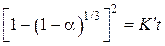которое известно как уравнение Яндера.
Оно является приближенным для частиц сферической формы, так как связь толщины слоя с радиусом непрореагировавшей части частицы малого размера оказывается более сложной.
Более строгий учет сферической симметрии может быть выполнен следующим образом. Уравнение (3.5) перепишем в виде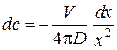 
. Интегрируя в приближении независимости скорости диффузионного потока от x
,
получаем
или 
(7)
Сопоставление уравнений (6) и (3) дает выражение для линейной скорости перемещения реакционной зоны
(8)
которое указывает на более сложную, чем из (6), зависимость линейной скорости от размера r непрореагировавшей части карбоната. На начальном этапе, когда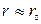 
и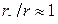 
сферическая симметрия частиц не проявляется, то есть линейная скорость, как и в предыдущем случае, обратно пропорциональна толщине оксидного слоя 
. Затем при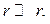 
с дальнейшим утолщением слоя продукта диссоциации (с уменьшением r) линейная скорость возрастает.
Интегрирование уравнения (8) и введение степени превращения 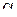через отношение (2) приводит к кинетическому уравнению
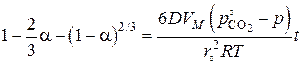(9)
Приведенное к форме
оно известно как уравнение Кранка, Гистлинга и Браунштейна. Это уравнение оказывается более точным по сравнению с уравнением Яндера, так как было учтено изменение объема сферы по ходу реакции.
Из уравнения (9) время полного завершения диссоциации карбоната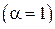 
(10)
Сравнение с уравнением (4) для времени завершения процесса в кинетическом режиме приводит качественно к тем же выводам. Однако для процесса в диффузионном режиме следует отметить более сильное влияние размера зерен карбоната и менее сильное влияние температуры, так как к сильному уменьшению 
за счет экспоненциального роста 
и 
с ростом температуры добавляется некоторое увеличение с ростом величины T, находящейся в числителе уравнения (10).
