2020-01-14
294
Для того чтобы упростить определение закона движения сложной системы, реальный механизм заменяют динамической моделью. Модель представляет собой стойку и вращающееся звено, называемое звеном приведения, инерционность которого определяется суммарным приведенным моментом инерции 
. На звено приведения действует суммарный приведенный момент сил 
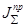. Параметры динамической модели 
и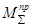 
определяют так, чтобы законы движения звена приведения динамической модели и движения начального звена реального механизма совпадали:
; 
.
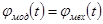В качестве начального звена механизма выбран кривошип 1. Таким образом, обобщенная координата для механизма 
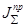. и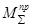 
определяются методом приведения сил и масс.
Определение суммарного приведенного момента
Метод приведения сил основан на равенстве элементарных работ и мгновенных мощностей приведенного момента, приложенного к модели, и реальных сил – к реальному механизму.
Для модели мощность 
, где 
, а для реального механизма 
, где 
- проекции на вертикаль скорости центра масс 
-го звена. Учитывая, что 
, а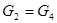 
, приравниваем мощность модели и реального механизма. Разделив равенство на скорость 
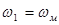начального звена, получаем
,
где 
- аналоги скоростей могут быть определены для каждого положения механизма из плана скоростей.
В данном случае приведенный момент сил сопротивления равен действительному моменту, т.к. приложен к входному звену и, в первом приближении, его можно считать постоянным. Однако его величина не задана, поэтому она определяется из условия установившегося режима работы.
