Комплексная проводимость двухполюсника

И 4.18	Определение. Комплексная проводимость двухполюсника – это величина, обратная его комплексному сопротивлению, . (4.9)
И 4.19	Следствие 1. Комплексная проводимость играет роль коэффициента пропорциональности между входным комплексным током и комплексным напряжением, приложенным к двухполюснику, , .

И 4.20

Следствие 2. Модуль комплексной проводимости равен полной проводимости двухполюсника, аргумент комплексной проводимости равен сдвигу фаз между напряжением и током с обратным знаком:

Доказательство следствия 2.

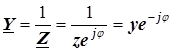где использовано определение полной проводимости (И 3.45).

И 4.21

Следствие 3. Действительная часть комплексной проводимости равна эквивалентной активной проводимости двухполюсника, а мнимая часть равна эквивалентной реактивной проводимости двухполюсника с обратным знаком: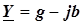

Доказательство следствия 3.

где использованы свойства эквивалентной активной проводимости и эквивалентной реактивной проводимости двухполюсника .

Для запоминания основных формул

(4.10)

можно использовать перевернутый треугольник проводимостей (рис. 3.8 и 4.5).

Рис 4.5. Треугольник проводимостей, приспособленный к формулам (4.10)

Комплексная проводимость двухполюсника с

Параллельным соединением резистора, катушки

И конденсатора

Считая известными входное напряжение и параметры электрической цепи (рис. 4.6), определим входной ток.

Рис. 4.6. Пример электрической цепи синусоидального тока с

параллельным включением элементов

По первому закону Кирхгофа

где - реактивная проводимость рассматриваемого двухполюсника; - индуктивная проводимость катушки; - емкостная проводимость конденсатора; - активная проводимость резистора.