Цели урока: научиться вычислять объем тел вращения с помощью определенного интеграла.
Повторить:
1. Формулу Ньютона-Лейбница для нахождения значения определенного интеграла
2. Таблицу первообразных.
Представьте некоторую плоскую фигуру на координатной плоскости. Данную фигуру можно ещё и вращать, причем вращать двумя способами:
– вокруг оси абсцисс 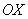 ;
;
– вокруг оси ординат  .
.
Пример 1
Вычислить объем тела, полученного вращением фигуры, ограниченной линиями  ,
,  вокруг оси
вокруг оси 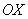 .
.
Решение:

Искомая плоская фигура заштрихована синим цветом, именно она и вращается вокруг оси 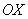 .
.
Объем тела вращения можно вычислить по формуле:
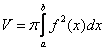
Вычислим объем тела вращения, используя данную формулу:

Ответ: 
Пример 2
Найти объем тела, образованного вращением вокруг оси 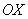 фигуры, ограниченной линиями
фигуры, ограниченной линиями  ,
,  ,
, 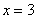
Решение: Выполним чертеж:

Объем тела вращения:

Ответ: 
Пример 3
Вычислить объем тела, полученного при вращении вокруг оси абсцисс фигуры, ограниченной линиями  ,
,  ,
,  и
и 
Решение: Изобразим на чертеже плоскую фигуру, ограниченную линиями  ,
,  ,
,  ,
,  , не забывая при этом, что уравнение
, не забывая при этом, что уравнение  задает ось
задает ось  :
:

Искомая фигура заштрихована синим цветом. При её вращении вокруг оси 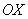 получается такой сюрреалистический бублик с четырьмя углами.
получается такой сюрреалистический бублик с четырьмя углами.
Объем тела вращения вычислим как разность объемов тел.
Сначала рассмотрим фигуру, которая обведена красным цветом. При её вращении вокруг оси 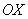 получается усеченный конус. Обозначим объем этого усеченного конуса через
получается усеченный конус. Обозначим объем этого усеченного конуса через  .
.
Рассмотрим фигуру, которая обведена зеленым цветом. Если вращать данную фигуру вокруг оси 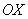 , то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через
, то получится тоже усеченный конус, только чуть поменьше. Обозначим его объем через  .
.
И, очевидно, разность объемов  – в точности объем нашего «бублика».
– в точности объем нашего «бублика».
Используем стандартную формулу для нахождения объема тела вращения:
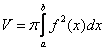
1) Фигура, обведенная красным цветом ограничена сверху прямой  , поэтому:
, поэтому:

2) Фигура, обведенная зеленым цветом ограничена сверху прямой  , поэтому:
, поэтому:
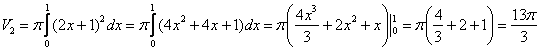
3) Объем искомого тела вращения: 
Ответ: 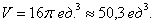
Пример 4
Вычислить объем тела, образованного вращением относительно оси 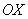 плоской фигуры, ограниченной линиями
плоской фигуры, ограниченной линиями  ,
,  , где
, где  .
.
Пример 4: Решение: Выполним чертеж:

Объем тела вращения вычислим как разность объемов при помощи формулы:

В данном случае:

Ответ: 
Вычисление объема тела, образованного вращением
плоской фигуры вокруг оси 
Пример 5
Дана плоская фигура, ограниченная линиями  ,
,  ,
,  .
.
1) Найти площадь плоской фигуры, ограниченной данными линиями.
2) Найти объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси  .
.
Решение: Задача состоит из двух частей. Начнем с площади.
1) Выполним чертёж:

Легко заметить, что функция  задает верхнюю ветку параболы, а функция
задает верхнюю ветку параболы, а функция  – нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».
– нижнюю ветку параболы. Перед нами тривиальная парабола, которая «лежит на боку».
Нужная фигура, площадь которой предстоит найти, заштрихована синим цветом.
Поэтому: 
Чем в данном случае плох обычный путь решения? Во-первых, получилось два интеграла. Во-вторых, под интегралами корни, а корни в интегралах – не подарок, к тому же можно запутаться в подстановке пределов интегрирования. На самом деле, интегралы, конечно, не убийственные, но на практике всё бывает значительно печальнее, просто я подобрал для задачи функции «получше».
Есть более рациональный путь решения: он состоит в переходе к обратным функциям и интегрированию по оси  .
.
Как перейти к обратным функциям? Грубо говоря, нужно выразить «икс» через «игрек». Сначала разберемся с параболой:

Этого достаточно, но убедимся, что такую же функцию можно вывести из нижней ветки:

Для самопроверки рекомендую устно или на черновике подставить координаты 2-3 точек параболы в уравнение  , они обязательно должны удовлетворять данному уравнению.
, они обязательно должны удовлетворять данному уравнению.
С прямой всё проще: 
Теперь смотрим на ось  : пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не прикол!). Нужная нам фигура лежит на отрезке
: пожалуйста, периодически наклоняйте голову вправо на 90 градусов по ходу объяснений (это не прикол!). Нужная нам фигура лежит на отрезке  , который обозначен красным пунктиром. При этом на отрезке
, который обозначен красным пунктиром. При этом на отрезке  прямая
прямая  расположена выше параболы
расположена выше параболы  , а значит, площадь фигуры следует найти по уже знакомой вам формуле:
, а значит, площадь фигуры следует найти по уже знакомой вам формуле:  . Что поменялось в формуле? Только буква, и не более того.
. Что поменялось в формуле? Только буква, и не более того.
! Примечание: Пределы интегрирования по оси  следует расставлять строго снизу вверх!
следует расставлять строго снизу вверх!
Находим площадь:
На отрезке 
 , поэтому:
, поэтому:

Обратите внимание, как я осуществил интегрирование, это самый рациональный способ, и в следующем пункте задания будет понятно – почему.
Для читателей, сомневающихся в корректности интегрирования, найду производные:

Получена исходная подынтегральная функция, значит интегрирование выполнено правильно.
Ответ: 
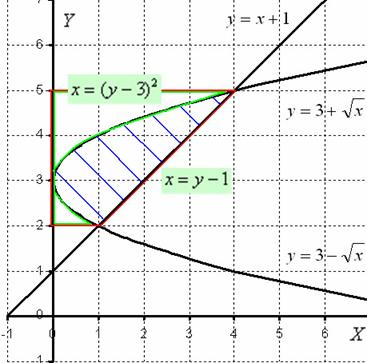
Итак, фигура, заштрихованная синим цветом, вращается вокруг оси  . В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
. В результате получается «зависшая бабочка», которая вертится вокруг своей оси.
Для нахождения объема тела вращения будем интегрировать по оси  . Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.
. Сначала нужно перейти к обратным функциям. Это уже сделано и подробно расписано в предыдущем пункте.
Очевидно, что объем тела вращения, следует найти как разность объемов.
Вращаем фигуру, обведенную красным цветом, вокруг оси  , в результате получается усеченный конус. Обозначим этот объем через
, в результате получается усеченный конус. Обозначим этот объем через  .
.
Вращаем фигуру, обведенную зеленым цветом, вокруг оси  и обозначаем через
и обозначаем через  объем полученного тела вращения.
объем полученного тела вращения.
Объем нашей бабочки равен разности объемов  .
.
Используем формулу для нахождения объема тела вращения:

В чем отличие от формулы предыдущего параграфа? Только в букве.

Ответ: 
Если эту же плоскую фигуру вращать вокруг оси 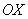 , то получится совершенно другое тело вращения, другого, естественно, объема.
, то получится совершенно другое тело вращения, другого, естественно, объема.
Пример 6
Дана плоская фигура, ограниченная линиями  ,
,  и осью
и осью 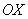 .
.
1) Перейти к обратным функциям и найти площадь плоской фигуры, ограниченной данными линиями, интегрированием по переменной  .
.
2) Вычислить объем тела, полученного вращением плоской фигуры, ограниченной данными линиями, вокруг оси  .
.
ответ 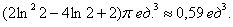 (тоже для любителей порешать).
(тоже для любителей порешать).
Пример 7
Вычислить объем тела, образованного вращением вокруг оси  фигуры, ограниченной кривыми
фигуры, ограниченной кривыми  и
и  .
.
Решение: Выполним чертеж:

Попутно знакомимся с графиками некоторых других функций. Такой вот интересный график чётной функции  ….
….
Для цели нахождения объема тела вращения достаточно использовать правую половину фигуры, которую я заштриховал синим цветом. Обе функции являются четными, их графики симметричны относительно оси  , симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси
, симметрична и наша фигура. Таким образом, заштрихованная правая часть, вращаясь вокруг оси  , непременно совпадёт с левой нештрихованной частью.
, непременно совпадёт с левой нештрихованной частью.
Перейдем к обратным функциям, то есть, выразим «иксы» через «игреки»:

Пример 6: Решение:
1) Выполним чертёж:
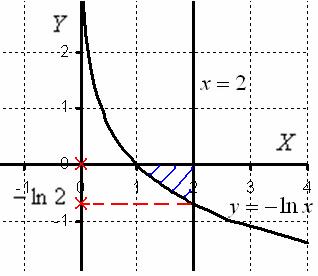
Перейдем к обратной функции:
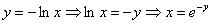
На отрезке 
 , поэтому:
, поэтому:

Ответ: 
2) Вычислим объем тела, образованного вращением данной фигуры, вокруг оси  .
.
Объем тела вращения найдем как разность объемов тел вращения при помощи формулы  :
:

Ответ: 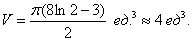
 2020-04-12
2020-04-12 1053
1053