Понятие первообразной функции и неопределенного интеграла

НЕОПРЕДЕЛЕННЫЙ ИНТЕГРАЛ

 

 

Во многих вопросах науки и техники, экономики приходится по известной производной восстанавливать саму функцию. Например, используя ленту скоростемера, мы находим функцию  скорости поезда в зависимости от времени. Но если мы хотим узнать, на каком километре пути находился поезд в тот или иной момент времени, нам нужно найти функцию 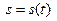 зависимости пройденного пути от времени. Как известно, производной функции  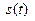будет функция , поэтому наша задача свелась к нахождению по заданной функции  неизвестной функции 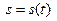, для которой производной будет . Таким образом, интегральное исчисление решает задачу нахождения самой функции по ее производной или дифференциалу.

Определение 1.1. Функция  в данном промежутке  называется первообразной функцией для функции , если на всем промежутке  функция  является производной для функции , т.е.  или, что то же самое,  служит для  дифференциалом, т.е. .

Пример 1.1.

Найти первообразную от функции .

Из определения 1.1. следует, что функция 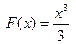 является первообразной, т.к. . Легко видеть, что если для данной функции существует первообразная, то эта первообразная не является единственной. В данном примере можно было взять в качестве первообразных следующие функции: или .

Теорема 1.1. Если в некотором (конечном или бесконечном) промежутке  функция  есть первообразная для , то и функция 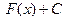, где  - любая постоянная, также будет первообразной. Обратно, каждая функция, первообразная для  в промежутке , может быть представлена в этой форме.

Определение 1.2. Если функция является первообразной для функции , то выражение 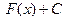называется неопределенным интегралом  и обозначается .

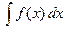Произведение  называется подынтегральным выражением, а функция  - подынтегральной функцией. Нахождение первообразной для данной функции называется интегрированием функции .

Таким образом, неопределенный интеграл представляет собой семейство функций .

С геометрической точки зрения неопределенный интеграл представляет собой совокупность (семейство) кривых, каждая из которых получается сдвигом одной из кривых параллельно самой себе вверх или вниз, т.е. вдоль оси

Замечание 1.1. Если функция непрерывна на промежутке , то для этой функции существует первообразная (а, следовательно, и неопределенный интеграл).

Из определения 1.2. следует, что:

1) .

2) .

3) .

 

Таблица основных неопределенных интегралов

 

Таблица 1

 

1.		16.
2.		17.
3.		18.
4.		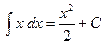19.
5.		20.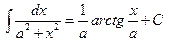
6.		21.
7.		22.
8.		23.
9.		24.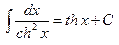
10.		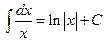25.
11.		26.
12.		27.
13.		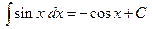28.
14.		29.
15.		30.