Апроксимація – підхід, за допомогою якого знаходиться аналітична функція  , що “найкращим чином” наближається до заданої табличної функції. Звичайно “найкращим чином” – це критерій, в якості якого використовується критерій середньо квадратичного відхилення (СКВ), заснований на тому, що сума квадратів відхилень аналітичної функції
, що “найкращим чином” наближається до заданої табличної функції. Звичайно “найкращим чином” – це критерій, в якості якого використовується критерій середньо квадратичного відхилення (СКВ), заснований на тому, що сума квадратів відхилень аналітичної функції  від експериментальної
від експериментальної  (при і=0, 1, …, k) повинна бути мінімальною:
(при і=0, 1, …, k) повинна бути мінімальною:

Апроксима́ція — наближене вираження одних математичних об'єктів іншими, простішими, наприклад, кривих ліній — ламаними, ірраціональних чисел — раціональними, неперервних функцій — многочленами.
В найпростішому випадку при п=1 матимемо:
 - формула лінійної інтерполяції,
- формула лінійної інтерполяції,
при п =2
 – формула квадратичного інтерполювання.
– формула квадратичного інтерполювання.
Доведемо для випадку п=1, що  . Тоді, матимемо систему
. Тоді, матимемо систему
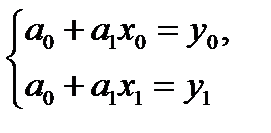
Розв’язуючи дану систему способом додавання, одержимо
 ,
,  .
.
Тоді 
Тоді 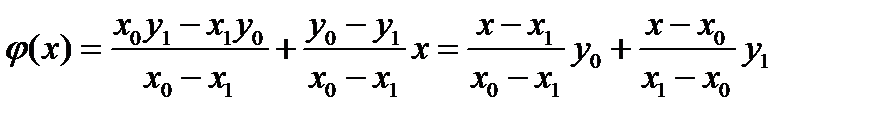 .
.
Зауваження: у випадку лінійної інтерполяції, припускаємо, що графіком функції є пряма, звідси приріст функції повинен бути пропорційним приросту аргументу. Якщо задане значення аргумента х знаходиться між наведеними в таблиці  і
і 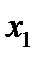 , де
, де 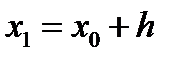 і
і  , тоді вважають, що
, тоді вважають, що

Можна записати формулу для оберненого інтерполювання:

Розглянемо приклади:
Приклад 1.
Провести інтерполяцію уявного економічного показника за даними таблиці
| Х | 0 | 1 | 2 | 3 |
| у | 6 | 4 | 1 | 3 |
Розв’язання:
За даними таблиці маємо квадратичне інтерполювання. Тоді беремо за  Виконавши алгебраїчні перетворення, одержимо:
Виконавши алгебраїчні перетворення, одержимо:

Дуже поширеним методом розв’язування задачі інтерполювання є метод найменших квадратів. Перед тим, як застосовувати його слід розв’язати систему рівнянь:

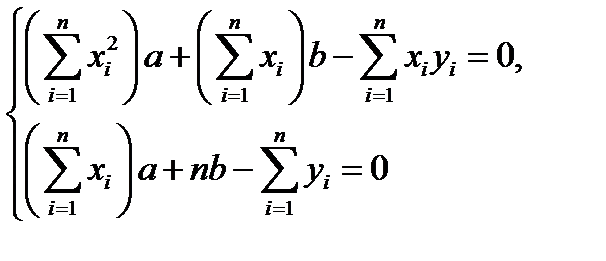 .
.
Маємо систему двох лінійних рівнянь з двома невідомими а і b. Розв’язуючи її, одержимо шукану функцію 

 2020-04-12
2020-04-12 164
164








