Множини, способи їх задання. Операції над множинами.
Одним з основних понять сучасної математики є поняття множини. У повсякденному житті ми постійно зустрічаємось з цим поняттям, розуміючи під ним зібрання, сукупність, колекцію речей, об’єднаних за деякими ознаками (зграя птахів, табун коней, колекція листівок). Прикладами множин у математиці є геометрична фігура, розв’язок нерівності чи систем нерівностей та ін.
За Г.Кантором множина – це сукупність, клас, група об’єктів, об’єднаних за якоюсь ознакою.
Множини позначаються великим латинськими літерами A,B,C,…,Z, а елементи множин – малими літерами a,b,c,…,x,y,z. Твердження про те, що елемент а належить множині А, записують у вигляді  . Коли навпаки – елемент а неналежить множині А, виконують такий запис:
. Коли навпаки – елемент а неналежить множині А, виконують такий запис:  . Якщо множини мають скінченну кількість елементів, то їх можна записати у вигляді
. Якщо множини мають скінченну кількість елементів, то їх можна записати у вигляді  . Нескінченні множини не можуть задаватись переліком їх елементів. Такі множини задають за допомогою характеристичної властивості їхніх елементів, тобто властивості, яку мають всі елементи цієї множини і тільки вони. Якщо Р(х) – скорочене позначення речення «елемент х має властивість Р», то множину М, елементи якої мають характеристичну властивість Р, записують так:
. Нескінченні множини не можуть задаватись переліком їх елементів. Такі множини задають за допомогою характеристичної властивості їхніх елементів, тобто властивості, яку мають всі елементи цієї множини і тільки вони. Якщо Р(х) – скорочене позначення речення «елемент х має властивість Р», то множину М, елементи якої мають характеристичну властивість Р, записують так:  .
.
Означення: Порожньою множиною  називається множина, яка не містить жодного елемента (тобто не існує елементів, що мають певну властивість).
називається множина, яка не містить жодного елемента (тобто не існує елементів, що мають певну властивість).
Означення: Дві множини А і В називаються рівними, якщо кожний елемент множини А є елементом множини В, і навпаки.
Означення: Множина А, що складається зі скінченної кількості елементів називається скінченною. Число елементів множини називають її потужністю і позначають М(А).
Означення: Множина А називається підмножиною множини В, якщо кожен елемент множини А є елементом множини В: 
Тоді можна записати, що А  А, Ø
А, Ø  А.
А.
Операції над множинами.
Означення: Об’єднанням двох множин А і В називається множина А  В, елементи якої належать хоча б одній із цих множин:
В, елементи якої належать хоча б одній із цих множин:
А  В ={ х| х
В ={ х| х  А або х
А або х  В}.
В}.
Означення: Перерізом двох множин А і В називається множина А  В, елементи якої належать як множині А, так і множині В:
В, елементи якої належать як множині А, так і множині В:
А  В = {х| х
В = {х| х  А і х
А і х  В}
В}
Означення: Різницею двох множин А і В називається множина А\В, елементи якої належать множині А і не належать множині В:
А\В = {х| х  А і х
А і х  В}.
В}.
Нехай А – підмножина множини Ω.
Означення: Різницю Ω\А називають доповненням множини А до множини Ω і позначають Ā.
Для операцій об’єднання, перерізу і віднімання множин справджуються такі властивості:
1. А  В = В
В = В  А; А
А; А  В= В
В= В  А (комутативність об’єднання і перерізу).
А (комутативність об’єднання і перерізу).
2. (А  В)
В)  С = А
С = А  (В
(В  С); (А
С); (А  В)
В)  С = А
С = А  (В
(В  С) (асоціативність об’єднання і перерізу).
С) (асоціативність об’єднання і перерізу).
3. (А  В)
В)  С = (А
С = (А  С)
С)  (В
(В  С) (дистрибутивність перерізу відносно об’єднання)
С) (дистрибутивність перерізу відносно об’єднання)
(А  В)
В)  С = (А
С = (А  С)
С)  (В
(В  С) (дистрибутивність об’єднання відносно перерізу).
С) (дистрибутивність об’єднання відносно перерізу).
4. (А\В)  С = (А
С = (А  С)\(В
С)\(В  С) (дистрибутивність перерізу відносно різниці.
С) (дистрибутивність перерізу відносно різниці.
5. Якщо А  В, то А
В, то А  В = В і А
В = В і А  В = А.
В = А.
Властивості 1 і 2 – очевидні. Доведемо властивість 3.
Доведення: Нехай  тоді
тоді 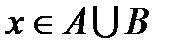 і
і  . Через те, що
. Через те, що  , то або
, то або  , або
, або  . Якщо
. Якщо  , то
, то  , але тоді
, але тоді  . Якщо
. Якщо  , то
, то 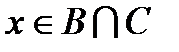 , але тоді
, але тоді  .
.
Отже, при  маємо
маємо  . А це означає, що
. А це означає, що  .
.
Нехай  , тоді або
, тоді або  , або
, або 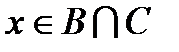 . Якщо
. Якщо  , то
, то  і
і  . Через те, що
. Через те, що  , то
, то 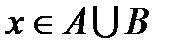 . Тоді
. Тоді  . Якщо
. Якщо 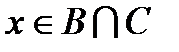 , то
, то  і
і  . Але тоді
. Але тоді 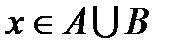 , а отже,
, а отже,  . Таким чином,
. Таким чином,  . Отже, (А
. Отже, (А  В)
В)  С = (А
С = (А  С)
С)  (В
(В  С).
С).
Властивість 4 доводиться аналогічно, тому доведете її самостійно.
Лема: Для будь-яких скінченних множин А і В виконується рівність:
 .
.
Доведення: Нехай А і В не перетинаються, тобто  . Тоді
. Тоді  , оскільки об’єднання розглядуваних множин утворюється додаванням усіх елементів однієї множини до елементів іншої.
, оскільки об’єднання розглядуваних множин утворюється додаванням усіх елементів однієї множини до елементів іншої.
Якщо множини А та В перетинаються, то кількість їх спільних елементів дорівнює  . Об’єднання множин А та В утворюється з елементів множини А та елементів множини В, що не є елементами множини А. Число таких елементів становить
. Об’єднання множин А та В утворюється з елементів множини А та елементів множини В, що не є елементами множини А. Число таких елементів становить  . Отже,
. Отже,  .
.
 2020-04-12
2020-04-12 158
158







