Пример. Для 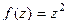 найти
найти 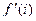 .
.
Решение. Способ 1.
Производная как от единой функции 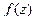 :
:
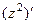 =
= 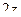 , что в точке
, что в точке 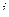 равно
равно 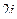 .
.
Способ 2.
По компонентам 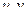 , достаточно лишь
, достаточно лишь 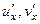 :
:
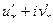 =
= 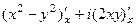 =
= 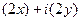 ,
,
в точке 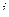 означает что в
означает что в 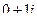 , т.е. данные функции надо вычислить в точке
, т.е. данные функции надо вычислить в точке 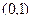 , что составляет
, что составляет 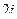 .
.
Теорема 2. 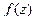 дифференцируемая функция
дифференцируемая функция 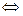 векторные поля
векторные поля
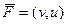 и
и 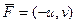 являются потенциальными.
являются потенциальными.
Доказательство. Вспомним условие потенциальности поля 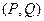 , а именно,
, а именно, 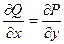 . Для векторного поля
. Для векторного поля 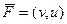 в таком случае,
в таком случае, 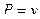 ,
, 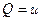 , и тогда условие потенциальности эквивалентно первому условию Коши-Римана
, и тогда условие потенциальности эквивалентно первому условию Коши-Римана 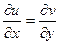 .
.
Для векторного поля 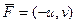 соответственно,
соответственно, 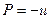 ,
, 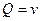 , и тогда условие потенциальности эквивалентно второму условию Коши-Римана:
, и тогда условие потенциальности эквивалентно второму условию Коши-Римана: 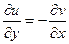 .
.
.
Определение. Если функция дифференцируема и в самой точке 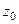 , и во всех точках некоторой её окрестности, то она называется аналитической в точке
, и во всех точках некоторой её окрестности, то она называется аналитической в точке  .
.
Пример. Для функции 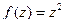 условия Коши-Римана выполняются независимо от точки, то есть во всех точках плоскости, тогда для каждой точки они автоматически выполнены и во всей её окрестности. Таким образом,
условия Коши-Римана выполняются независимо от точки, то есть во всех точках плоскости, тогда для каждой точки они автоматически выполнены и во всей её окрестности. Таким образом, 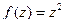 аналитическая во всех точках комплексной плоскости.
аналитическая во всех точках комплексной плоскости.
Различие понятий аналитичности и дифференцируемости видно на другом примере.
Пример. 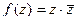 . Распишем её через
. Распишем её через 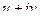 .
.
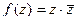 =
= 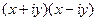 =
= 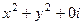 . Здесь
. Здесь 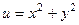 ,
, 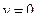 .
.
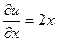 ,
, 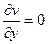 .
.
1-е условие Коши-Римана выполняется только при 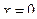
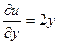 ,
, 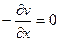 .
.
2-е условие Коши-Римана выполняется только при 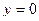 .
.
Таким образом, единственная точка в плоскости, где выполнены условия Коши-Римана, это (0,0). Но ни в одной точке из её окрестности они не выполняются, а только в одной изолированной точке 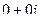 . То есть, в начале координат функция дифференцируемая, но не аналитическая.
. То есть, в начале координат функция дифференцируемая, но не аналитическая.
Теорема 3. Если функция является аналитической в некоторой области D, то для каждой из её частей (действительной и мнимой) 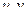 в этой области выполняется уравнение Лапласа:
в этой области выполняется уравнение Лапласа:
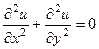 и
и 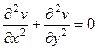 .
.
Доказательство.
Запишем 2 условия Коши-Римана. Одно продифференцируем по переменной  , а второе по
, а второе по 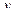 :
:
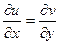
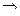
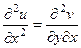
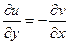
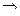
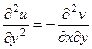 .
.
Сложим теперь эти 2 равенства, но при этом смешанные производные 2 порядка от 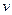 при этом совпадают, они вычитаются и дают 0.
при этом совпадают, они вычитаются и дают 0.
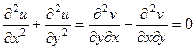 . Итак,
. Итак, 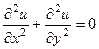 .
.
Теперь снова запишем условия Коши-Римана, 1-е дифференцируем по 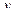 , а второе по
, а второе по  .
.
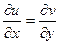
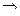
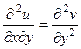
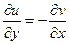
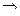
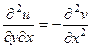 .
.
Теперь вычтем из 1-го равенства 2-е.
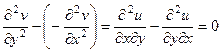 , тогда
, тогда 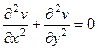 .
.
Пример. 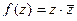 =
= 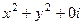 . Здесь для
. Здесь для 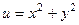 не верно уравнение Лапласа:
не верно уравнение Лапласа: 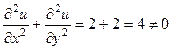 .
.
Пример. 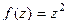 =
= 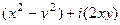 . Уравнение Лапласа для обеих частей функции:
. Уравнение Лапласа для обеих частей функции:
1) 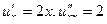 ,
, 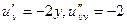 , в сумме 0.
, в сумме 0.
2) 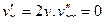 ,
,  , 0+0=0.
, 0+0=0.
ЛЕКЦИЯ № 9. 11.03.2020
Теорема 4. Условия Коши-Римана эквивалентны условию 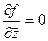 .
.
Доказательство. Вспомним, что 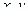 можно выразить через
можно выразить через 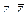 таким образом:
таким образом: 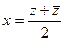 ,
, 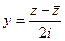 . Сделаем это в функциях
. Сделаем это в функциях 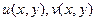 .
.
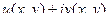 =
= 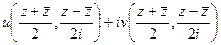 .
.
Таким образом, функция стала выражена через два аргумента 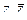 , а значит, можно искать частную производную по
, а значит, можно искать частную производную по 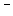 .
.
Вспомним формулу полной производной (из 1 семестра) для случая композиции типа 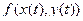 :
: 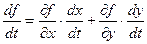 . Найдём производные от
. Найдём производные от 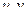 по
по 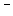 этим методом, причём здесь тоже промежуточные переменные
этим методом, причём здесь тоже промежуточные переменные 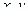 .
.
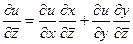 ,
, 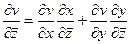 .
.
При этом такие компоненты как 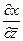 и
и 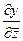 можно найти
можно найти
из формул 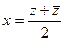 ,
, 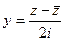 , а именно:
, а именно:
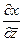 =
= 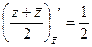 ,
, 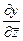 =
= 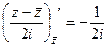 . Таким образом,
. Таким образом,
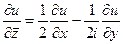 ,
,  .
.
Тогда 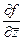 =
= 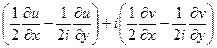 =
=
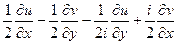 =
= 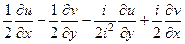 =
=
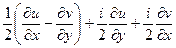 =
= 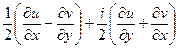 .
.
Выполнение условий Коши-Римана 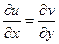
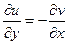
в данном случае как раз и эквивалентно тому, что в обеих скобках нули, то есть 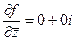 .
.
□
Итак, как видим, наличие 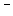 в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии
в составе функции приводит к недифференцируемости. Впрочем, то же верно и при наличии 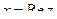 или
или 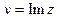 , в составе которых есть элемент
, в составе которых есть элемент 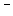 .
.
Так, например, 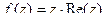 не является аналитической.
не является аналитической.
 2020-04-07
2020-04-07 147
147








