Поскольку действительная и мнимая части взаимосвязаны условиями Коши-Римана, то достаточно одной её части, чтобы восстановить вторую часть, и далее всю функцию 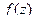 .
.
Например, нам известна  . Тогда
. Тогда 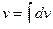 =
= 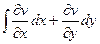 , это криволинейный интеграл 2 рода для векторного поля
, это криволинейный интеграл 2 рода для векторного поля 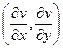 от фиксированной точки, например (0,0) до произвольной
от фиксированной точки, например (0,0) до произвольной 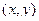 . Нам неизвестны эти частные производные, как и сама функция
. Нам неизвестны эти частные производные, как и сама функция 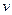 , однако их можно заменить на известные, по условиям Коши-Римана.
, однако их можно заменить на известные, по условиям Коши-Римана.
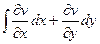 =
= 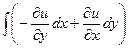 и далее вычислить.
и далее вычислить.
Итак, алгоритм:
1. Проверить выполнение уравнения Лапласа (иначе  или
или 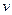 не может быть частью какой-то единой комплексной функции).
не может быть частью какой-то единой комплексной функции).
2. Вычислить криволинейный интеграл.
3. В полученной функции 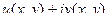 выразить
выразить 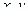 по формулам:
по формулам: 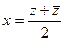 ,
, 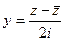 . При правильном вычислении сократятся все
. При правильном вычислении сократятся все  и останется только
и останется только 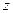 .
.
Пример. Дано 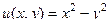 . Найти мнимую часть и восстановить вид функции
. Найти мнимую часть и восстановить вид функции 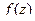 .
.
Сначала проверяем уравнение Лапласа.
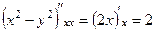 ,
, 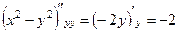 , сумма 2-й производных равна 0, то есть
, сумма 2-й производных равна 0, то есть 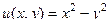 является одной из компонент комплексной функции.
является одной из компонент комплексной функции.
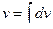 =
= 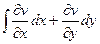 =
= 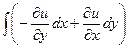 , где
, где 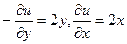 .
.
Итак, найдём криволинейный интеграл 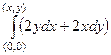 . Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля.
. Сделаем это с помощью интегрирования по ломаной, как при вычислении потенциала поля. 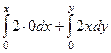 =
= 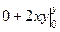 =
= 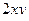 .
.
Далее, в выражение 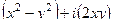 подставим
подставим 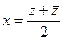 ,
, 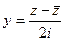 .
.
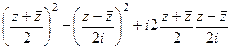 =
= 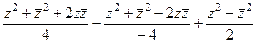 =
=
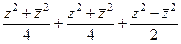 =
= 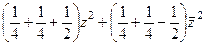 =
= 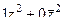 =
= 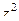 . Итак,
. Итак, 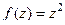 .
.
 2020-04-07
2020-04-07 660
660








