Вычисляем расширенную неопределённость

Согласно заданию значение вероятности охвата P = 0,95, которое соответствует «результатам измерения общего назначения».

Анализируя входные величины, отмечаем, что имеют место две составляющие суммарной неопределенности, одна из которых определена по тира А и имеет нормальный закон распределения, а другая – по типу В и имеет равномерный закон распределения.

В этом случае коэффициент охвата принимаем равным квантилю распределения Стьюдента при вероятности охвата Р   и эффективном числе степеней свободы ν_eff, определяемом по формуле

 

 

Подставив числовые значения, получим:

 

ν_eff = (22-1)(0.405/0.284)⁴ = 86.

Принимаем значение коэффициента охвата, равным k = 2

Определяем расширенную неопределённость по формуле:

U(Y) = k×u(Y).                                                  (7)

Получаем значение расширенной неопределённости:

U(Y) = 2×0.405 = 0,91 Ом.

Округляем данное значение по правилам округления результатов измерений, и получаем окончательное значение расширенной неопределённости:

U(Y) = 0,9 Ом.

6 Записываем результат измерения с учётом неопределённости.

Y = y ± U(Y) = (483,2  ± 0,9) Ом.

Измеренное значение сопротивления равно (483,2  ± 0,9) Ом,, где число, стоящее после знака ± расширенная неопределенность U(Y) = k×u(Y), полученная для суммарной стандартной неопределённости 0,405 и коэффициента охвата k = 2, соответствующего уровню доверия 95 % для t-распределения с v = 86 степенями свободы.                                 

Рекомендуемая литература:

1 ГОСТ Р 34100.3-2017. Руководство ИСО/МЭК 98-3:2008. Неопределенность измерения. Часть 3. Руководство по выражению неопределенности измерений

2 Захаров И.П. Неопределенность измерений для чайников и … начальников: Учебное пособие / И.П. Захаров. – Харьков: 2013. – 56 с.

3 Бронштейн И.Н. Справочник по математике для инженеров и учащихся вузов / И.Н. Бронштейн, К.А. Семендяев. - М.: Наука, 1986.- 544 с.

4 Шишкин, И.Ф. Теоретическая метрология. Ч. 1. Общая теория измерений: Учебник для вузов / И.Ф. Шишкин. – СПб.: Питер, 2010. – 190 с.

                 Раздел 3. «Преобразование и обработка сигналов»

 

Авторы задач: Щепетов Александр Григорьевич, профессор РГУ нефти и газа им. И.М. Губкина, e-mail: a-shchepetov@mail.ru, Ермолкин Олег Викторович, профессор  РГУ нефти и газа им. И.М. Губкина, e-mail ove@mail.ru, Дьяченко Юрий Николаевич, доцент Санкт-Петербургского политехнического университета Петра Великого, e-mail: ydko@mail.ru., Барат Вера Александровна, доцент НИУ МЭИ, e-mail  vera.barat@mail.ru

 

Общая характеристика: задания относятся к задачам преобразования и обработки измерительных сигналов.

 

                          Безынерционное преобразование случайного сигнала

На вход нелинейного безынерционного ИУ с известной функцией преобразования 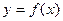 поступает случайный сигнал 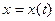, одномерная функция плотности распределения вероятностей (ПРВ) которого  известна. Требуется определить статистические характеристики выходного сигнала: ПРВ , математическое ожидание  и дисперсию . Пусть функция  обладает свойством изоморфизма, т.е. существует однозначная обратная функция (рис.1)

                                          .                                                                   (1)

 

 

                                                                                                                       Рис. 1.

Тогда событие  равносильно событию , что означает равенство вероятностей этих событий. Поэтому площади заштрихованных фигур на рис. 1 равны друг другу

                                       .                                                               (2)     

Из этого уравнения можно определить ПРВ выходного сигнала

                 , или .                              (3)

Зная ПРВ выходного сигнала, можно определить все статистические характеристики этого сигнала, в том числе его математическое ожидание  и дисперсию  

                      ,  .                                   (4)

Их можно вычислить также по формулам, не требующим знания функции , что можно использовать для контроля правильности расчетов

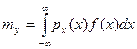                            ,                            (5)

Если обратная статическая характеристика ИУ является неоднозначной и имеет N ветвей, то вместо формулы (3) нужно пользоваться общей формулой

                                 ,                                                       (6)

где  - k - ая ветвь обратной статической характеристики ИУ (1). При правильных расчетах должно выполняться условие нормировки ПРВ. Покажем пример решения такой задачи [1].

Задача 3.1. (Щепетов А.Г.) На вход безынерционного ИУ с квадратичной характеристикой  поступает случайный сигнал , ПРВ которого имеет вид

 

                                            ,                                                    (7)

 

т.е. входной сигнал на интервале  имеет равномерное распределение (рис. 2, а). Нужно определить статистические характеристики выходного сигнала: плотность распределения вероятностей , математическое ожидание  и дисперсию .

 

Решение:   Обратная статическая характеристика ИУ  является неоднозначной, так как имеет две ветви (рис.2,б)

                                       и .

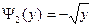Поэтому формула (6) содержит два слагаемых и имеет вид

                     ,

где следует записать

 

                         ,

                                                     

                    

 

Учитывая, что         ,        можно записать

                                .

 

 

На рис. 2, в показан график этой функции. Условие нормировки ПРВ выходного сигнала выполняется. Действительно,

 

 

                                             .

 

 

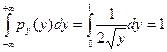                                                                                                    Рис. 2

 

 

Математическое ожидание и дисперсию выходного сигнала вычислим по формулам (4)

 

                          ,

                          .

 

Вычисления по формулам (5) приводят к таким же результатам

 

                    ,

                       .

 

                   Инерционное преобразование периодического сигнала

Задача 3.2. (Ермолкин О.В., Щепетов А.Г.) Определить реакцию прибора с передаточной функцией ,                                                    

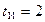на периодический сигнал, представляющий собой последовательность однополярных прямоугольных импульсов (меандр) амплитуды   и длительности с, следующих друг за другом с интервалом 2 с (рис.1).

               

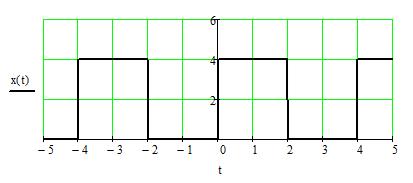
                                                                        Рис. 1

 

Покажем решение этой задачи разными способами [1].

 

Способ 1. Первый способ решения задачи основан напредставлении периодического входного сигнала в форме тригонометрического ряда Фурье

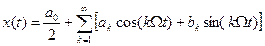                         ,                                       (1)

где - коэффициенты Фурье. В соответствии с принципом суперпозиции, реакция линейного ИУ на такой сигнал равна сумме реакций на каждую из составляющих ряда (1) в отдельности, т.е.

                                      ,                                (2)

где     - реакция ИУ на единичный ступенчатый сигнал ;  и 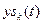- реакции ИУ на гармонические составляющие сигнала  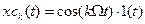и  соответственно.

Полагая начальные условия нулевыми, можно записать

 

;   ; .

 

Следовательно 

           ,       (3)

 

где - переходная функция ИУ;  - оригиналы соответствующих изображений, зависящие от вида передаточной функции ИУ  и формы базового импульса входного сигнала. Покажем применение этих формул для решения рассматриваемой задачи.

 

Решение: Коэффициенты Фурье входного сигнала вычислим по формулам

 

                               , где ,                                  

                                , где .                              

где 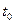  – произвольное число, которое можно выбирать из соображений удобства вычисления. Значение этого числа обычно выбирают так, чтобы функция  на отрезке   не имела особенностей. Полагая в приведенных формулах , , .В результате получим

                , , , то есть 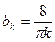, где        (4)                      

 

Следовательно, разложение рассматриваемого входного сигнала 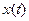 в тригонометрический ряд Фурье содержит только нечетные гармоники и имеет вид

 

                    .                       (5)

 

Вычислим переходную функцию ИУ

 

                            (6)

 

и найдем оригиналы слагаемых ряда (1)

 

                          , где ,

 

Соответствующие оригиналы  определим с помощью теоремы разложения. Для этого воспользуемся разложением

 

                                .                                (7)

 

Умножая обе части этого разложения на  и приравнивая коэффициенты в обеих частях полученного равенства при одинаковых степенях , получим систему уравнений

                               , , ,

 

решая которую, найдем значения коэффициентов разложения (7)

                                                    .

Таким образом 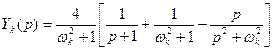           .                          (8)

 

Переходя в (1) к оригиналам, окончательно получим

 

              .           (9)

 

С течением времени (при  ) в выходном сигнале ИУ исчезают составляющие с экспоненциальным множителем и он становится периодическим. (рис. 2). Этот установившийся периодический выходной сигнал имеет вид

 

                 .               (10)

 

На рис. 2 показаны графики рассматриваемых входного и выходного сигналов ИУ. Входной сигнал (меандр) показан сплошной кривой 1, установившийся выходной сигнал (10) - пунктирной кривой 2. Видно, что процесс установления выходного сигнала практически завершается уже по истечение половины периода входного сигнала  с. В общем случае это время соизмеримо с длительностью переходного процесса.

        

 

 

Рис. 2

 

К сожалению, установившийся выходной сигнал (10) получен в форме ряда.

Способ 2. Установившееся периодическое решение (10) можно получить, если воспользоваться полученными ранее результатами анализа реакции ИУ на гармонический сигнал единичной амплитуды

                                                          ,                                            (11)

Установившаяся реакция линейного инерционного ИУ на такой сигнал имеет вид (3.56)

 

                                          ,                                           (12)

 

где 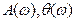 - соответственно модуль и аргумент комплексной частотной характеристики ИУ

                                    , .                                    (13)

 

Учитывая (1), вместо (10) для установившегося выходного сигнала получаем

                                                                                 

        .        (14)

 

В рассматриваемом случае имеем

                          , , , , ,

              , .

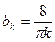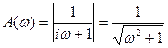Следовательно

                              .                   (15)

Учитывая соотношения

                          и ,

несложно доказать, что прежнее решение (10) и найденное решение (15) совпадают друг с другом.

 

Способ 3. Периодический сигнал можно представить в виде суммы базовых импульсов, сдвинутых друг относительно друга по оси времени на величину, кратную периоду сигнала , т.е.

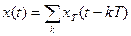                                                    ,                                               (16)

где - базовый импульс сигнала. Реакция линейного ИУ на такой входной сигнал равна сумме реакций ИУ на каждый из импульсов в отдельности, т.е.

 

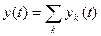                                                       ,                                                       (17)

где - реакция ИУ на ый «сдвинутый» базовый импульс входного сигнала

                                                      .

В рассматриваемом случае можно записать

                                                   ,                                            (18)

где  - единичная ступенчатая функция времени (1.10). Соответствующее изображение по Лапласу базового импульса равно

                                 .                        (19)

Тогда изображение реакции ИУ на первый импульс имеет вид

 

                      ,         (20)

где                                      .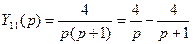

 

Переходя в (20) к оригиналам, найдем реакцию ИУ на первый импульс входного сигнала

 

                           .                   (21)

 

то есть,                               (22)                    

 

На рис. 3 показаны графики базового импульса входного сигнала 1 и реакции ИУ на этот импульс 2, построенной по формуле (22). Реакция ИУ на второйимпульс входного сигнала равна  и т.д., реакция на  ый импульс

 

                                              .                                                  (23)

 

Суммируя отклики ИУ на все импульсы входного сигнала, получим выходной сигнал ИУ

 

                                     ,                                       (24)

где  вычисляется по формуле (21).

         Рис. 3.

 

Выполняя суммирование этого ряда, можно показать, что с течением времени выходной сигнал ИУ оказывается периодическим и имеет тот же период , что и входной сигнал, а его базовый импульс  вычисляется по формулам

                                   ,                                (25)

 

где - время, отсчитываемое от момента установления периодического выходного сигнала ИУ. Формулы (25), в отличие от (13) и (14), определяют установившийся выходной сигнал ИУ в аналитическом виде.

 

Способ 4. В заключение рассмотрим еще один способ решения задачи, позволяющий достаточно просто (без суммирования рядов) определить установившийся периодический выходной сигнал ИУ в аналитическом виде. Этот способ основан на методе вариации произвольных постоянных, который применяется при решении неоднородных дифференциальных уравнений.

       Для этого запишем, учитывая вид передаточной функции ИУ , операционное уравнение, связывающее изображения входного и выходного сигналов ИУ

 

                               , т.е. .                       (26)

 

Переходя во временную область и полагая, что начальные условия, наложенные на выходной сигнал, нулевые (т.е. считая, что 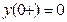), получим дифференциальное уравнение ИУ

                                                        .                                             (27)

Вновь перейдем в операторную область, полагая, что упомянутые выше начальные условия ненулевые (т.е., полагая, что ). В этом случае вместо (26) получим другое уравнение

                                            ,                                       (28)

из которого следует

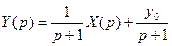                                              .                                           (29)

 

Оригинал, соответствующий первому слагаемому в формуле (П2.67), найдем с помощью теоремы умножения. Второе слагаемое имеет табличный оригинал, то есть

                                             .                                      (30)

Выбор начального условия (т.е. выбор значения , входящего в формулу (24)) подчиним условию периодичности установившегося выходного сигнала

                                                                .                                                   (31)

Кроме того, будем считать, что период этого сигнала совпадает с периодом входного сигнала, т.е. . Тогда, раскрывая (30), получим уравнение

 

                                                    .                                (32)

Отсюда найдем . Возвращаясь к (30), получим                        

                                       .                                  (33)

Первое слагаемое в формуле (33) есть ранее найденная реакция ИУ (21) на базовый импульс входного сигнала, т.е. вместо (33) можно записать

 

                                 .                    (34)

 

После приведения подобных членов формулы (34) совпадают с формулами (25).

 

Примечание:  

1) Если  , то вместо (30) можно получить

                                      

При увеличении коэффициента k снижается постоянная времени ИУ. В этом случае форма установившегося выходного сигнала ИУ приближается к форме кходного сигнала.

2) при решении задачи для ИУ - го порядка изображение (29) содержит  произвольных постоянных , а условие периодичности (31) заменяется 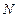 условиями вида .

 

Литература

1. Щепетов А.Г., Дьяченко Ю.Н. Преобразование измерительных сигналов: учебник и практикум для академического бакалавриата. – М.: Издательство Юрайт, 2017. – 270 с.