План:
1. Точечные и интервальные оценки.
2. Интервальные оценки параметров нормального распределения.
1. Точечной называют оценку, которая определяется одним числом. Все оценки, рассмотренные выше, являются точечными. При выборке малого объема точечная оценка может значительно отличаться от оцениваемого параметра, то есть приводить к грубым ошибкам. По этой причине при небольшом объеме выборки следует пользоваться интервальными оценками.
Интервальной называют оценку, которая определяется двумя числами – началом и концом интервала. Интервальные оценки позволяют установить точность и надежность оценок.
Пусть  - это оценка неизвестного оцениваемого параметра
- это оценка неизвестного оцениваемого параметра  . Пусть
. Пусть  - это некоторое положительное число. Если выполняется неравенство
- это некоторое положительное число. Если выполняется неравенство
 ,
,
то говорят, что интервал  покрывает неизвестный параметр
покрывает неизвестный параметр  .
.
Определение 1. Надежностью оценки  параметра
параметра  для заданного
для заданного  называют вероятность того, что интервал
называют вероятность того, что интервал  покрывает параметр
покрывает параметр  , и обозначают в виде
, и обозначают в виде
 .
.
Иными словами,  есть мера доверия вычисленной оценке
есть мера доверия вычисленной оценке  .
.
Определение 2. Доверительным интервалом называют найденный по данным выборки интервал  , который покрывает неизвестный параметр
, который покрывает неизвестный параметр  с заданной надежностью
с заданной надежностью  .
.
Надежность  задается по условию задачи и обычно принимается равной 0,95, или 0,99, или 0,999.
задается по условию задачи и обычно принимается равной 0,95, или 0,99, или 0,999.
2. Как уже было отмечено выше, для задания нормального закона распределения необходимо знать математическое ожидание и среднее квадратическое отклонение. Рассмотрим доверительные интервалы для этих числовых характеристик.
Доверительный интервал для математического ожидания (генеральной средней) имеет вид
 ,
,
 - выборочная средняя;
- выборочная средняя;
 - объем выборки;
- объем выборки;
 - при большом объеме выборки;
- при большом объеме выборки;
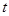 - значение аргумента функции Лапласа, при котором она равна
- значение аргумента функции Лапласа, при котором она равна  , то есть
, то есть  , где
, где  - заданная надежность. Аргумент
- заданная надежность. Аргумент 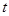 находится по таблицам значений функции Лапласа (приложение 2).
находится по таблицам значений функции Лапласа (приложение 2).
Пример. Найти интервальную оценку признака  генеральной совокупности, то есть доверительный интервал для математического ожидания, если известно, что
генеральной совокупности, то есть доверительный интервал для математического ожидания, если известно, что 
Решение.
Для того чтобы воспользоваться приведенной выше формулой, найдем  из равенства
из равенства
 , следовательно
, следовательно 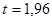 .
.
Тогда, доверительный интервал будет иметь вид
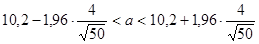 ;
;
 ;
;
 .
.
Таким образом, с вероятностью 95% можно утверждать, что неизвестна генеральная средняя может находится в промежутке от 9,09 до 11,31.
Приведенная выше формула доверительного интервала математического ожидания будет справедлива только при большом объеме выборки, то есть если 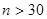 . В противном же случае, равенство
. В противном же случае, равенство  не будет выполнятся и считают
не будет выполнятся и считают 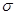 неизвестной величиной. Таким образом, если объем выборки не большой
неизвестной величиной. Таким образом, если объем выборки не большой  , то доверительный интервал для генеральной средней будет иметь вид:
, то доверительный интервал для генеральной средней будет иметь вид:
 ,
,
где  - это исправленное среднее квадратическое отклонение;
- это исправленное среднее квадратическое отклонение;
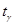 - это число, взятое из таблицы (приложение 3), и зависящее от объема выборки
- это число, взятое из таблицы (приложение 3), и зависящее от объема выборки  и заданной надежности
и заданной надежности  , то есть
, то есть  .
.
Пример. На контрольных испытаниях 16 осветительных ламп были получены результаты: среднее время горения лампы составляет 3000 часов и  ч. Считая, что срок службы каждой лампы является нормально распределенной с.в., определить с надежностью 0,99 доверительный интервал для генеральной средней.
ч. Считая, что срок службы каждой лампы является нормально распределенной с.в., определить с надежностью 0,99 доверительный интервал для генеральной средней.
Решение.  .
.
Найдем число 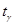 по таблице, получим
по таблице, получим  .
.
Тогда, доверительный интервал будет иметь вид
 ;
;
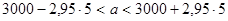 ;
;
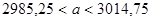 .
. 
Таким образом, с вероятностью 99% можно утверждать, что истинное среднее время горения лампы будет заключено в промежутке от 2985,25 часов до 3014,75 часов.
Доверительный интервал для оценки среднего квадратического отклонения 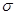 вычисляется по формуле
вычисляется по формуле
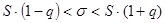 ,
,
где  - это исправленное среднее квадратическое отклонение;
- это исправленное среднее квадратическое отклонение;
 - это табличное значение, которое зависит от объема выборки
- это табличное значение, которое зависит от объема выборки  и заданной надежности
и заданной надежности  , то есть
, то есть  (приложение 4).
(приложение 4).
Вычисление числовых характеристик выборки с помощью условных вариант.
План:
1. Условные варианты.
2. Обычные, начальные и центральные эмпирические моменты.
3. Условные эмпирические моменты. Отыскание центральных моментов через условные.
1. Предположим, что варианты выборки расположены в возрастающем порядке, то есть в виде вариационного ряда.
Определение 1. Равноотстоящими называют варианты, которые образуют арифметическую прогрессию с шагом  .
.
Пример. 5, 10, 15, 20, …
Определение 2. Условными называют варианты, определяемые равенством
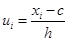 ,
,
где  - это ложный нуль (новое начало отсчета),
- это ложный нуль (новое начало отсчета),  - шаг, то есть разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
- шаг, то есть разность между любыми двумя соседними первоначальными вариантами (новая единица масштаба).
Замечание: 1) В качестве ложного нуля можно принять любую из вариант, но удобнее принимать ту варианту, которая расположена примерно в середине вариационного ряда или ту варианту, которой соответствует наибольшая частота.
2) Варианте, которая принимается в качестве ложного нуля, соответствует условная варианта, равная нулю.
Пример. Найти условные варианты следующего статистического распределения
 | 23,6 | 28,6 | 33,6 | 38,6 | 43,6 |
 | 5 | 20 | 50 | 15 | 10 |
Решение. Пусть  (так как соответствует наибольшая частота и находится в середине вариационного ряда).
(так как соответствует наибольшая частота и находится в середине вариационного ряда).
Найдем шаг:  .
.
Найдем условные варианты:
 ;
;
 ;
;
 ;
;
 ;
;
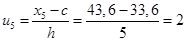 .
.
Получаем не большие целые числа, с которыми проще работать, чем с первоначальными. Составим вариационный ряд в условных вариантах.

 | -2 | -1 | 0 | 1 | 2 |
 | 5 | 20 | 50 | 15 | 10 |
2. Для вычисления сводных характеристик выборки удобно пользоваться эмпирическими моментами, определения которых аналогичны определениям соответствующих теоретических моментов (математическое ожидание, дисперсия). В отличие от теоретических эмпирические моменты вычисляют по данным наблюдений.
Определение 3. Обычным эмпирическим моментом порядка  называют среднее значение
называют среднее значение  степеней разности
степеней разности  , то есть
, то есть
 ,
,
где  - наблюдаемые варианты,
- наблюдаемые варианты,
 - соответствующие частоты вариант;
- соответствующие частоты вариант;  - ложный ноль.
- ложный ноль.
Определение 4. Начальным эмпирическим моментом порядка 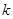 называют обычный момент порядка
называют обычный момент порядка  , вычисленный при условии, что
, вычисленный при условии, что  , то есть
, то есть
 .
.
В частности, если  , то получаем начальный момент первого порядка вида
, то получаем начальный момент первого порядка вида  , который равен выборочной средней. Таким образом
, который равен выборочной средней. Таким образом 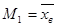 .
.
Определение 5. Центральным эмпирическим моментом порядка 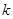 называют обычный момент порядка
называют обычный момент порядка  , вычисленный при условии, что
, вычисленный при условии, что  , то есть
, то есть
 .
.
В частности, если  , то получаем центральный момент второго порядка вида
, то получаем центральный момент второго порядка вида  , который равен выборочной дисперсии. Таким образом
, который равен выборочной дисперсии. Таким образом  .
.
Выражая центральные моменты через обычные моменты, получаем следующие равенства:
 ;
;
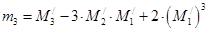 ;
;
 .
.
3. Вычисление центральных моментов требует довольно громоздких вычислений. Чтобы упрости расчеты, заменяют первоначальные варианты условными и находят условные эмпирические моменты различных порядков.
Определение 6. Условным эмпирическим моментом порядка 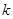 называют начальный момент порядка
называют начальный момент порядка  , вычисленный для условных вариант, то есть
, вычисленный для условных вариант, то есть
 .
.
Найдем условный момент первого порядка
 ,
,
или  , или
, или  ,
,
или  .
.
Таким образом, для того чтобы найти выборочную среднюю, достаточно вычислить условный момент первого порядка, умножить его на шаг и к результату добавить ложный нуль.
Выразим обычные моменты через условные
 ,
,
или  .
.
Таким образом, для того чтобы найти обычный момент порядка 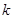 , достаточно вычислить условный момент того же порядка
, достаточно вычислить условный момент того же порядка  и умножить его на
и умножить его на 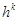 .
.
Найдя же обычные моменты, легко найти центральные моменты по приведенным выше формулам. В итоге получим удобные для вычислений формулы, выражающие центральные моменты через условные:
 ;
;
 ;
;
 .
.
Как было доказано выше, 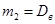 . Тогда, формулу для вычисления дисперсии можно переписать в виде
. Тогда, формулу для вычисления дисперсии можно переписать в виде
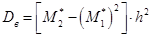 .
.
 2020-04-12
2020-04-12 3174
3174

 -
-