2020-04-12
3630
План:
1. Понятия генеральной и выборочной дисперсий и методы их расчета.
2. Оценка генеральной дисперсии по исправленной выборочной.
1. Для того чтобы охарактеризовать рассеяние значений признака 
генеральной совокупности вокруг своего среднего значения, вводят числовую характеристику, называемую дисперсией.
Пусть изучается дискретная генеральная совокупность относительно количественного признака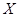 
.
Определение 1. Генеральной дисперсией 
называют среде арифметическое квадратов отклонений значений признака генеральной совокупности от их среднего значения 
.
Если все значения признака генеральной совокупности объема 
различны и равны 
, то
.
Если же значения признака 
имеют соответственно частоты 
, причем 
, то
.
Пример. Генеральная совокупность задана таблицей распределения
| 2 | 4 | 5 | 6 |
| 8 | 9 | 10 | 3 |
Найти генеральную среднюю.
Решение.
Найдем генеральную среднюю.
.
Найдем генеральную дисперсию.
.
Кроме дисперсии для характеристики рассеяния значений признака генеральной совокупности вокруг своего среднего значения пользуются числовой характеристикой, называемой средним квадратическим отклонением.
|
|
|
Определение 2. Генеральным средним квадратическим отклонением называют корень квадратный из генеральной дисперсии и обозначают в виде
.
Пусть для изучения генеральной совокупности относительно количественного признака 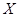произведена выборка объема 
.
Определение 3. Выборочной дисперсией 
называется среднее арифметическое квадратов отклонений наблюдаемых значений выборки от выборочной средней 
.
Если все значения признака 
выборки объема различны, то
.
Если же значения признака имеют соответственно частоты 
, причем 
, то
.
Пример. Выборочная совокупность задана таблицей распределения
| 1 | 2 | 3 | 4 |
| 20 | 15 | 10 | 5 |
Найти выборочную дисперсию.
Решение.
Найдем выборочную среднюю.
.
Найти выборочную дисперсию.
.
Определение 4. Выборочным средним квадратическим отклонением называют корень квадратный из выборочной дисперсии и обозначают в виде
.
Записанные выше формулы вычисления выборочной и генеральной дисперсии можно упрости, используя следующую теорему.
Теорема: Дисперсия равна разности между средним квадратов значений признака и квадратом общей средней, то есть
, где
и 
.
Пример. Вычислим дисперсию, пользуясь теоремой, для статистического распределения заданного в предыдущем примере. Найдем выборочное среднее квадратическое отклонение.
Решение.
Общая средняя уже известна 
.
|
|
|
Найдем среднюю квадратов значений признака:
.
Тогда 
и 
- это среднее отклонение от среднего значения выборки, то есть от числа .
2. Пусть из генеральной совокупности в результате 
независимых наблюдений над количественным признаком 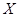извлечена повторная выборка объема 
, где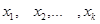 
- это значения признака 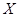и 
соответствующие им частоты, причем .
Требуется по данным выборки оценить (приближенно найти) неизвестную генеральную дисперсию . Если в качестве оценки генеральной дисперсии принять выборочную дисперсию, то эта оценка будет приводить к ошибкам, давая заниженное значение генеральной дисперсии. Для избежания таких ошибок вводят числовую характеристику, называемую исправленной дисперсией, которую вычисляют по формуле
.
Итак, в качестве оценки генеральной дисперсии принимают исправленную дисперсию.
Для оценки же среднего квадратического отклонения генеральной совокупности используют исправленное среднее квадратическое отклонение, которое равно корню квадратному из исправленной дисперсии и обозначается в виде
.
Пример. Найти выборочную и исправленную дисперсии для следующего статистического распределения
| 1 | 2 | 5 | 8 | 9 |
|
| 3 | 4 | 6 | 4 | 3 |
Решение.
Найдем выборочную среднюю.
.
Найдем выборочную дисперсию по определению.
.
Тогда 
.
