Метод произведений дает удобный способ вычисления условных моментов различных порядков вариационного ряда с равноотстоящими вариантами. Зная же условные моменты, нетрудно найти начальные и центральные эмпирические моменты. В частности, методом произведений удобно вычислять выборочную среднюю и выборочную дисперсию. Целесообразно пользоваться расчетной таблицей, которая составляется следующим образом:
1) в первый столбец таблицы записывают выборочные (первоначальные) варианты, располагая их в возрастающем порядке;
2) во второй столбец записывают частоты вариант, складывают их и полученную сумму записывают в последнюю клетку столбца;
3) в третий столбец записывают условные варианты 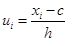 ;
;
4) умножают частоты на условные варианты 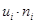 и записывают в четвертый столбец, находят сумму полученных произведений и записывают в последнюю клетку столбца;
и записывают в четвертый столбец, находят сумму полученных произведений и записывают в последнюю клетку столбца;
5) умножают частоты на квадраты условных вариант 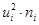 и записывают в пятый столбец, находят сумму полученных произведений и записывают в последней клетке столбца;
и записывают в пятый столбец, находят сумму полученных произведений и записывают в последней клетке столбца;
6) умножают частоты на квадраты условных вариант, увеличенных каждая на единицу, и записывают произведения  в шестой столбец, находят сумму полученных произведений и записывают в последнюю клетку столбца.
в шестой столбец, находят сумму полученных произведений и записывают в последнюю клетку столбца.
Замечание: Шестой столбец нужен для контроля вычислений. Если выполняется равенство
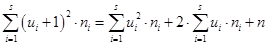 ,
,
то вычисления произведены правильно.
После того, как расчетная таблица заполнена и проверена правильность вычислений, находят условные моменты
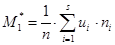 и
и 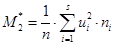 .
.
Затем вычисляют выборочную среднюю и выборочную дисперсию по формулам
 и
и 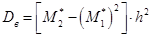 .
.
Пример. Найти методом произведений выборочную среднюю и выборочную дисперсию для следующего статистического распределения
| xi | 10,2 | 10,4 | 10,6 | 10,8 | 11 | 11,2 | 11,4 | 11,6 | 11,8 | 12 |
| ni | 2 | 3 | 8 | 13 | 25 | 20 | 12 | 10 | 6 | 1 |
Решение. Найдем условные варианты, для этого выберем ложный нуль.
Пусть 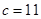 , так как она расположена в середине таблицы и ей соответствует наибольшая частота.
, так как она расположена в середине таблицы и ей соответствует наибольшая частота.
Тогда 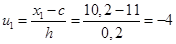 ;
;
 ;
;  ;
;
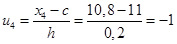 ;
; 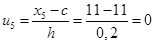 ;
;

Построим расчетную таблицу.
| xi | ni | ui | ui · ni | ui2· ni | (ui+1)2· ni |
| 10,2 10,4 10,6 10,8 11 11,2 11,4 11,6 11,8 12 | 2 3 8 13 25 20 12 10 6 1 | -4 -3 -2 -1 0 1 2 3 4 5 | -8 -9 -16 -13 0 20 24 30 24 5 | 32 27 32 13 0 20 48 90 96 25 | 18 12 8 0 25 80 108 160 150 36 |
| ∑ | 100 | - | 57 | 383 | 597 |
Выполним проверку 597==383+2·57+100. вычисления выполнены верно.
Вычислим условные моменты первого и второго порядков:
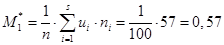 ;
;
 .
.
Так как разность между двумя соседними первоначальными вариантами равна 0,2, то шаг 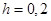 .
.
Вычислим выборочную среднюю и выборочную дисперсию:
 ;
;
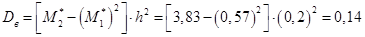 .
.
Замечание: Приведенная выше таблица может быть дополнена большим количеством столбцов в случае, если необходимо будет вычислить условные моменты более высоких порядков.
 2020-04-12
2020-04-12 403
403







