Примеры решения задач

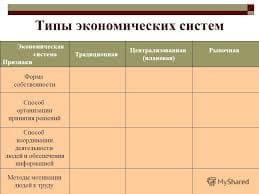
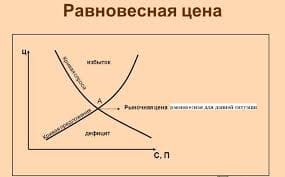
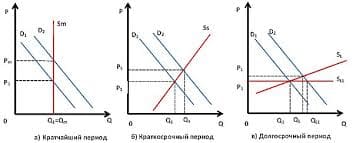
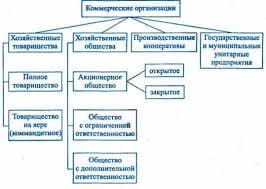
Задача 1. Точка вращается вокруг оси Oz с угловой скоростью w, находясь от неё на постоянном расстоянии a > 0 и одновременно поднимается вверх вдоль Oz с постоянной скоростью b > 0. Составьте уравнение траектории данной точки, если в момент времени t = 0 она находилась на оси Ox (винтовая линия). Проверить регулярность получившегося пути.

Решение. Из условия задачи вытекает, что проекция данной точки на плоскость Oxy описывает окружность радиуса a в этой плоскости. При этом угол, который определяет положение проекции точки на

окружности (отсчитываемый от оси Ox) изменяется по закону j = wt. Поэтому координаты x и y изменяются по закону

x = a cos wt, y = a sin wt.

Координата z задаёт «высоту» точки над «горизонтальной» плоскостью Oxy. Она изменяется с постоянной скоростью b: z = bt. Отсюда окончательно получаем уравнение траектории:

 

x = a cos wt, = a sin wt, (20) = bt.

 

Находим координаты вектора с ¢, а затем квадрат его длины:

с ¢(- aw sin wt, aw cos wt, b),

| с ¢|² = (aw)²sin²wt + (aw)²cos²wt + b² = (aw)² + b² > 0.

 

Следовательно, путь является регулярным при любом значении параметра.

Задача 2. Окружность радиуса a на плоскости катится без скольжения по оси Ox. На окружности отмечена точка M.

1. Составить уравнение траектории данной точки (циклоида).

2. Проверить регулярность получившегося пути.

3. Найти длину одной арки циклоиды.

4. Найти естественный параметр и записать уравнение циклоиды в естественной параметризации на каком-либо одном её участке.

5. Вычислить кривизну циклоиды и определить в каких точках кривизна достигает экстремальных значений.

Решение. 1. Предположим, что окружность повернулась на угол j и касается оси Ox в точке K. Пусть O¢ - её центр. Введём вспомогательную декартову СК O¢x¢y¢, которая получается из Oxy переносом начала координат в точку O¢. Окружность катится по оси Ox без скольжения. Поэтому длина отрезка OK равна длине дуги KM, т.е.

равна aj, если угол исчисляется в радианах. Отсюда O¢(aj, a) и формулы замены координат:

 

x = x¢+ aj,

y = y¢+ a.

 

В новой СК по чертежу легко найти координаты точки M:

 

x¢= - a·cos(j -) = - a·sin j, y¢= a·sin(j -) = - a·cos j.

 

Отсюда получаем уравнение циклоиды:

 

x = a(j - sin j),

y = a(1 - cos j).

 

Заметим, что вид уравнения (знаки и расположение синуса и косинуса) зависит от того, какой именно угол выбран в качестве параметра.

2. Находим координаты вектора с ¢, а затем квадрат его длины:

с ¢(a(1 - cos j), a sin j),

| с ¢|² = a²(1 - 2cos j + cos²j + sin²j) = 2a²(1 - cos j).

Решаем уравнение

 

| с ¢|² = 0 Û cos j = 1 Û j = 2pk.

 

Следовательно, путь является регулярным при любых значениях параметра, кроме j=2pk. Очевидно, этим значениям соответствуют точки на оси Ox; отмеченная точка принимает их положение когда окружность завершает полный оборот.

3. Длина кривой вычисляется по формуле (9) § 5. Одна арка циклоиды соответствует изменению параметра 0£j£2p. Поэтому её длина

 

L =| c ¢(t)| dt = dt = a dt = 2a|sin |dt =

= 2asin dt = 2a(- 2cos )|= 4a(- cos p + cos 0) = 8a.

 

При вычислениях мы учитывали, что на промежутке [0, 2p] выполнено sin ³ 0.

4. Естественный параметр находится по формуле (10) § 5, где знак «+» или «-», а так же t_o (в нашем случае j_o) мы можем выбрать по желанию. Выберем j_o= 0 и знак «+». Тогда

= 2a sin dt = - 4a cos  |= 4a , если jÎ[0, 2p];= 4a(- cos | + cos |) = 4a , если jÎ[2p, 4p].

Также и на всех последующих промежутках [2pn, 2p(n +1)] получается своя отдельная формула. Поэтому запишем уравнение с естественным параметром только для участка кривой, соответствующего jÎ[0, 2p]. Имеем s = 4a . Выражаем из этого уравнения j и подставляем в уравнение циклоиды.

 

cos  = 1- Þ j = 2arccos , sÎ[0, 8a];  = =  , j = 2sin  ·cos  =,

 - cos j = 2sin²  = (8as - s²) =  . = 2a arccos -, = s -.

. Кривизна плоской кривой вычисляется по формуле (11¢) § 6. Находим координаты вектора с ², а затем вычисляем отдельно числитель и знаменатель из формулы (11¢):

 

с ²(a sin j, a cos j),

= a²(sin²j - cos j(1 - cos j)) =

= a²(1 - cos j) = 2a²sin² .

| с ¢|³ = (2a²(1 - cos j))^3/2 = (4a²sin² )^3/2 = 8a³|sin³ |

Подставляем найденное в формулу (11¢) и получаем

 

k =

 

Можно сделать вывод, что кривизна стремится к +¥ при приближении точки к оси Ox (j -® 2pn, nÎ Z) и достигает минимального значения при sin  = ±1, т.е. в самых верхних точках арок циклоиды (j = pm, mÎ Z).

Задача 3. Для винтовой линии

 

x = a cos t,

y = a sin t,

z = bt:

. Найти длину одного витка (tÎ[0, 2p]), найти естественный параметр и записать уравнение в естественной параметризации.

2. Вычислить кривизну и кручение.

3. Записать натуральные уравнения.

Решение. 1. с ¢(- a sin t, a cos t, b),

 

| c ¢(t)| = = (*) = | c ¢(t)| dt = dt = 2p. = | c ¢(t)| dt = dt = t  Þ t =.

 

Подставляем это значение в уравнение кривой и получаем уравнение в естественной параметризации:

 

x = a cos,

y = a sin, = .

. Кривизна и кручение вычисляются по формулам (11) и (15) из § 6 соответственно. Нам понадобятся вторые и третьи производные:

с ²(- a cos t, - a sin t, 0), с ²¢(a sin t, - a cos t, 0).

Находим вектор с ¢´ с ², а затем его квадрат:

с ¢´ с ² = - a sin t a cos t b = (ab sin t) i - (ab cos t) j + a² k.

 a cos t - a sin t 0

| с ¢´ с ²|² = (ab sin t)² + (ab cos t) ² + a⁴ = a²(a² + b²).

 

При подстановке в формулу для кривизны не забываем извлечь корень:

 

k = = =.

 

Обращаем внимание, что | c ¢| уже вычислен выше (см. (*)).

В числителе формулы (15) стоит смешанное произведение. Его можно вычислить непосредственно:

 

 a sin t a cos t b

с ¢ с ² с ¢¢¢ = - a cos t - a sin t 0 = ba²,

а можно воспользоваться определением: с ¢ с ² с ¢¢¢ = (с ¢´ с ²)· с ¢¢¢. В различных задачах наиболее удобным может оказаться тот или иной способ. Знаменатель для кручения уже найден. Итак,

 

k= = =.

. Для того, чтобы записать натуральные уравнения k = k(s), kk(s) кривой, необходимо в формулах для кривизны и кручения сделать замену параметра t на параметр s. В нашем случае кривизна и кручение постоянны, поэтому и заменять нечего. Натуральные уравнения нашей винтовой линии имеют вид:

 

k =, k=.

Задача 4. Кривая на плоскости задана уравнением в неявном виде:

 

ln(x² + y²) - x²y = 0.

 

Составить уравнение касательной и нормали к данной кривой в точке A (1, 0).

Решение. Сначала подставим координаты точки A в уравнение и убедимся, что она действительно принадлежит кривой. Обозначим левую часть уравнения j(x, y). Находим вектор градиента для функции j(x, y) и значение градиента в точке A:

 

grad j = =;

grad_Aj = (2, - 0,5).

Тогда уравнение касательной и нормали в точке A (см. формулы (3), (6) из § 3):

 

(x - 1) - 0,5 (y - 0) = 0 Û 4x - y - 4 = 0 (касательная);

= Û x - 4y - 1 = 0 (нормаль).

Задача 5. В какой точке касательная к кривой

 

x = e^t,

g: y = - e^-t,

z = t

 

параллельна плоскости p: x + y - 2z - 5 = 0? В этой точке составить уравнение касательной прямой, нормальной плоскости, соприкасающейся плоскости, бинормали. Найти векторы, составляющие репер Френе в найденной выше точке.

Решение. Направляющим вектором касательной служит вектор c ¢(t) = (e^t, e^-t, 1). Вектор (1, 1,-2) - это вектор нормали к плоскости. Касательная будет параллельна плоскости p (или будет лежать в ней), если c ¢(t)^ Û c ¢(t)· = 0. Последнее уравнение в координатах имеет вид e^t + e^-t - 2 = 0.

Решая это уравнение находим, что t = 0. Подставим найденное значение параметра в уравнение кривой и находим точку A (1, -1, 0). Именно в этой точке требуется составить все указанные в условии задачи уравнения. Поэтому находим c ¢(0) = (1, 1, 1). Касательная прямая и нормальная плоскость (см. (1) и (5) из § 3):

= = Û x - 1 = y + 1 = z.

(x - 1) + 1 (y + 1) + 1 (z - 0) = 0 Û x + y + z = 0.

 

Поскольку точка A не лежит в плоскости p, то и найденная касательная к кривой g в этой плоскости не лежит.

Находим вектор второй производной в точке A:

c ²(t) = (e^t, - e^-t, 0), c ²(0) = (1, - 1, 0)

 

и составляем уравнение соприкасающейся плоскости (см. (7) § 4):

 

x - 1 y + 1 z

1 1 = 0 Û x + y - 2z = 0.

- 1 0

 

Попутно мы нашли координаты вектора c ¢(0)´ c ²(0) = (1, 1, - 2), который является направляющим для бинормали. Отсюда уравнение бинормали:

 

= =.

 

Далее находим (c ¢(0)´ c ²(0))´ c ¢(0) = (3, - 3, 0) (тот факт, что он оказался коллинеарным c ²(0) - это случайное совпадение, связанное с тем, что у нас получилось c ²(0)^ c ¢(0)). Находим длины

 

| с ¢(0)| =, | c ¢(0)´ c ²(0)| =  | с ¢(0)| | c ¢(0)´ c ²(0)|= 3 Þ

t , n , b =.

Задача 6. Найти линию, по которой касательные к кривой

 

x = cos t,

g: y = sin t, = e^t,

 

пересекают плоскость Oxy.

Решение. Нам необходимо составить уравнение касательной к кривой в произвольной точке, т.е. при произвольном значении параметра t = t_o. Находим направляющий вектор касательной при t = t_o:

c ¢(t_o) = (- sin t_o, cos t_o, e^to).

 

Координаты точки, которая используется в

уравнении касательной, получатся если в уравнение кривой g подставить t = t_o. Отсюда получаем уравнение касательной:

 

= =. (*)

 

Плоскость Oxy задаётся уравнением z = 0. Подставляем это равенство в (*) и получаем:

 

= = -1.

 

Выражаем отсюда x и y, и заменяем t_o на t (т. к. значение t_o является произвольным). Окончательно получаем уравнение искомой кривой:

x = cos t + sin t,

y = sin t - cos t.

На самом деле, эта кривая является окружностью. Используя тригонометрические формулы, мы можем преобразовать уравнение:

 

x = cos (t -), y = sin(- t).

 

Сделаем здесь замену параметра: u = p/4 - t. Она является допустимой, т.к. du/dt = -1 ¹ 0. Получим уравнение окружности радиуса с центром в начале координат:

 

x = cos u,

y = sin u.

 

Можно иначе проверить, что наша кривая - это окружность:

 

x² + y² = (cos t + sin t)² +(sin t - cos t)² = 2cos²t + 2sin²t = 2.

Задача 7. Докажите, что следующая кривая является плоской и составьте уравнение плоскости в которой она лежит.

 

x = (t-1)³, y = (t+1)³, z = t².

Решение. Согласно теореме 7 из § 6 нам требуется доказать, что кручение данной кривой тождественно равно нулю. При этом, достаточно доказать, что числитель в формуле для кручения равен нулю: с ¢ с ² с ¢¢¢=0. Находим:

 

(t-1)² (t+1)² 2t (t-1)² (t+1)² 2t

с ¢ с ² с ¢¢¢= 2 (t-1) 2 (t+1) 2 = 4 (t-1) (t+1) 1 =

2 2 0 1 1 0

= 4 ((t+1)² - 2t (t+1) + 2t (t-1) - (t-1)²) º 0.

 

Плоскость в которой лежит кривая - это её соприкасающаяся плоскость. Мы уже доказали, что кривая плоская. Поэтому мы можем составить уравнение соприкасающейся плоскости в любой её фиксированной точке, например, при t_o=0. Находим точку на кривой, соответствующую данному значению параметра и векторы производных в этой точке:

 

M_o(- ,, 0), с ¢(0)=(1, 1, 0), с ²(0)=(-2, 2, 2).

 

Составляем уравнение соприкасающейся плоскости, заменяя при этом вектор с ²(0) на коллинеарный ему вектор (-1, 1, 1):

 

= 0 Û x - y + 2z + = 0.

 

Задача вроде бы решена. Но мы не учли один «тонкий» момент: во всех ли точках существует у данной кривой кручение? При t=1 мы получаем с ¢(1)=(0, 4, 2), с ²(1)=(0, 4, 2). Значит, в этой точке с ¢´ с ²= и кривизна кривой тоже равна нулю. В такой точке кривая может переходить из одной плоскости в другую. Поэтому следует сделать проверку: подставить x, y, z из уравнения кривой в уравнение плоскости. Должно получиться тождество.

Задача 8. Вычислить угол между кривыми

а) g₁: y = sin x и g₂: y = cos x;

б) g₃: и g₄:

в точке из пересечения.

Решение. а) Находим ординату точки пересечения кривых:

 

sin x = cos x Û x = + pn, nÎ Z.

 

Возьмём в начале одно значение x = и найдём производные y₁¢ (для g₁) и y₂¢ (для g₂) при данном значении x:

 

y₁¢() = cos  =, y₂¢() = - sin  = -.

 

Эти значения задают угловые коэффициенты k₁ и k₂ касательных к кривым в точке их пересечения. Угол между касательными в точке пересечения кривых и есть угол между кривыми (по определению). Угол между прямыми находится о формуле

 

tg q = = = = 2.

 

Нетрудно проверить, что и в других точках пересечения тоже получается tg q = 2.

Ответ: q = arctg 2.

б) Находим значения параметров в точке пересечения:

 

Û

 

Умножаем последнее уравнение на e^5t и получаем e^6,5t = 1 Þ t = 0, t =1.

Обозначим c (t) = (t², t³), d (t) = (e^t, e^-5t). Тогда касательные векторы к данным кривым - это c ¢(t) = (2t, 3t²), d ¢(t) = (e^t, -5e^-5t). Касательные векторы в точке пересечения - c ¢(1) = (2, 3), d ¢(0) = (1, -5). Эти векторы являются направляющими векторами для касательных прямых в точке пересечения кривых g₃ и g₄. Косинус угла между прямыми равен модулю косинуса угла между их направляющими векторами:

множество гомеоморфизм скалярный дифференциальный

cos a = = = =.

Ответ: a = 45º.

Литература

 

1. Klingenberg W. A course of differential geometry / W. Klingenberg.-N.Y. - Heidelberg - Berlin: Springer-Verlag, 1976.

2. Погорелов А.В. Геометрия / А.В. Погорелов. - М.: Наука, 1984.

3. Александров А.Д. Геометрия / А.Д. Александров, Н.Ю. Нецветаев.- М.:Наука, 1990.

. Феденко А.С. Дифференциальная геометрия / И.В. Белько, В.И. Ведерников, А.С. Феденко. - Мн.: Изд-во БГУ, 1982.

. Дубровин Б.А. Современная геометрия: Методы и приложения / Б.А. Дубровин, С.П. Новиков, А.Т. Фоменко. - М.: Наука, 1979.

. Александров П.С. Введение в теорию множеств и общую топологию / П.С. Александров. - М.: Наука, 1977.

. Воднев В.Т. Сборник задач и упражнений по дифференциальной геометрии / В.Т. Воднев и др. - Мн.: Вышэйшая школа, 1970.

. Атанасян Л.С. Сборник задач по геометрии / Л.С. Атанасян и др. - М.: Просвещение, 1975.

. Мищенко А.С. Курс дифференциальной геометрии и топологии / А.С. Мищенко, А.Т. Фоменко. - М.: Изд-во МГУ, 1980.

. Постников М.М. Лекции по геометрии. Семестр III. Гладкие многообразия / М.М. Постников. - М. Наука, 1987.