2020-05-11
95
Задание №1. Решить уравнение 
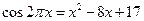
Образец решения: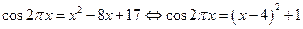 
. Оценим левую и правую части уравнения: 
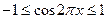и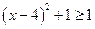 
. Следовательно, равенство достигается, если 
. Решая второе уравнение системы, получаем 
. Подставляем это значение в первое уравнение и убеждаемся в верности равенства. Следовательно, корень исходного уравнения.
Ответ: .
Для решения используем следующие знания:
ü Выделение полного квадрата из квадратичного трехчлена.
ü Свойство ограниченности функции синус: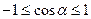 
.
ü Свойство ограниченности квадратичной функции: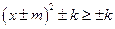 
.
ü Формулы решения частного тригонометрического уравнения
Задание №2. Решить уравнение 
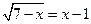
Образец решения: Подбором находим, что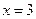 
- корень уравнения. Убеждаемся, что других корней нет, поскольку левая часть уравнения – это убывающая функция, а правая – возрастающая функция.
Ответ: .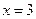
Для решения используем следующие знания:
ü Метод подбора решения уравнения.
ü Свойство убывающей функции: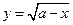 
.
ü Свойство возрастающей функции: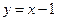 
.
ü Теорема о монотонности функций.
|
|
|
Задание №3. Решить уравнение 
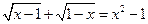
Образец решения: Рассмотрим ОДЗ уравнения, имеем ОДЗ: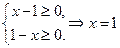 
. Таким образом, область допустимых значений состоит из одного числа. Останется проверить, является ли число 
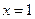- корень исходного уравнения. Убеждаемся в этом, подставляя 
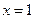в исходное уравнение: 
. Равенство верное, значит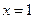 
- корень исходного уравнения.
Ответ: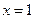 
.
Для решения используем следующие знания:
ü Область допустимых значений функции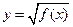 
: ОДЗ(f): 
.
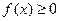Задание №4. Решить уравнение 
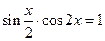
Образец решения: Так как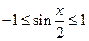 
и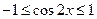 
, то произведение 
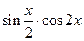может равняться 1 лишь при выполнении одной из двух систем 
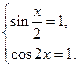или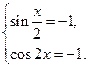 
Решим первую систему 
.
Решим вторую систему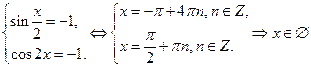 
Ответ: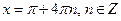 
.
Для решения используем следующие знания:
ü Свойство ограниченности функции синус: 
.
ü Свойство ограниченности функции синус: 
.
ü Решение простейших тригонометрических уравнений
ü Выбор корней уравнения на тригонометрическом круге среди серий корней простейших уравнений.
