Канонический базис Якоби квадратичной формы

Теорема. Ортонормированный базис пространства, состоящий из собственных векторов симметрической матрицы,, является каноническим базисом квадратичной формы, а выражение – ее каноническим видом в базисе.

Доказательство.

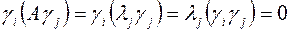, если 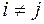, так как 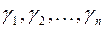– ортогональная система векторов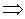 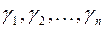– канонический базис квадратичной формы .

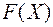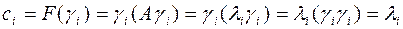, так как векторы системы 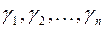нормированы, то , .

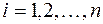Будем говорить, что матрица 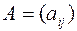удовлетворяет условию Якоби, если определители

, ,

называемые угловыми минорами матрицы не равны нулю. Очевидно, что , .

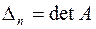Обозначим через матрицу

.

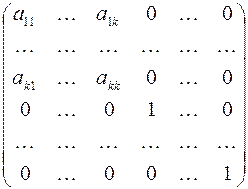Вычислим определитель этой матрицы, разлагая ее по последнему столбцу, затем также по последнему столбцу разложим полученный определитель и т.д.

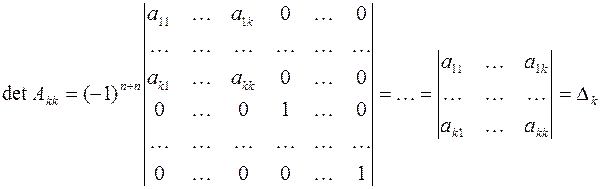
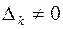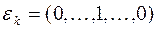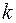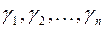Из условия , следует, что и, значит, каждая система уравнений , , где – –й вектор диагональной системы, имеет единственное решение , . Система векторов называется системой векторов Якоби матрицы , которая удовлетворяет условию Якоби.