2014-02-09
1784
Квадратичная форма отрицательно определена тогда и только тогда, когда главные миноры матрицы четного порядка положительны, а главные миноры матрицы нечетного порядка отрицательны.
Квадратичная форма положительно определена тогда и только тогда, когда главные миноры матрицы положительны.
Доказательство: Докажем первое утверждение.
Необходимость. Дано, что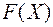 
положительно определена. Покажем, что все угловые миноры матрицы 
отличны от нуля. Допустим обратное, и пусть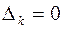 
. Тогда согласно Лемме найдется такой ненулевой вектор 
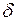, что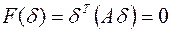 
. Однако это противоречит положительной определенности квадратичной формы.
Итак, матрица удовлетворяет условию Якоби, поэтому можно построить систему векторов Якоби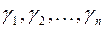 
, которая является каноническим базисом 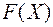, причем выражение 
–
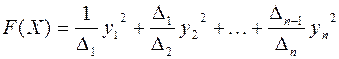ее канонический вид в базисе 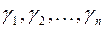. Теперь из положительной определенности квадратичной формы и первого утверждения доказанной ранее теоремы следует, что 
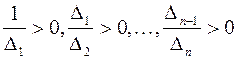, и значит, что 
.
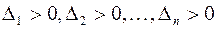Достаточность. Если 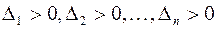, то угловые миноры матрицы отличны от нуля и можно построить канонический базис квадратичной формы 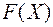, в котором –
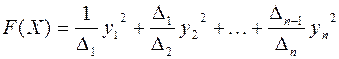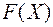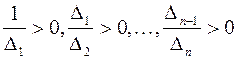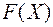канонический вид квадратичной формы . Поскольку , то положительно определена.
Аналогично доказывается второе утверждение теоремы.
В общем случае кривая второго порядка в базисе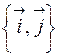 
описывается уравнением 
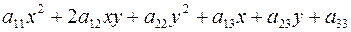. Ее первые три слагаемые образуют квадратичную форму 
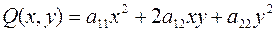с матрицей
.
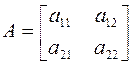Задача о приведении кривой 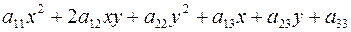к каноническому виду сводится к задаче о приведении к каноническому виду квадратичной формы 
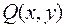этой кривой.
Пусть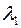 
и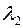 
– собственные значения матрицы , а 
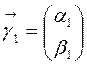и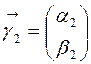 
– ортонормированные собственные векторы матрицы , соответствующие собственным значениям 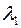и .
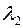Ортонормированные векторы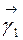 
и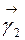 
называются главными направлениями этой кривой.
Пусть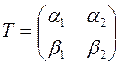 
является матрицей перехода от ортонормированного базиса 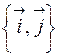к ортонормированному базису 
.
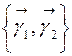Тогда ортогональное преобразование
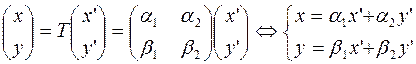
приводит квадратичную форму 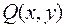к каноническому виду 
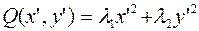, а уравнение кривой – к виду 
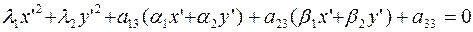в прямоугольной декартовой системе координат 
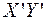, оси которой направлены вдоль векторов 
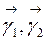, а начало совпадает с точкой 
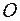системы координат 
.
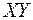Выделив в этом уравнении полные квадраты, получим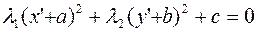 
, где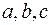 
– некоторые числа. Осуществив параллельный перенос системы координат 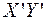в новое начало 
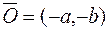, получим канонический вид уравнения 
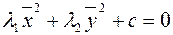в системе координат 
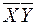. В зависимости от чисел 
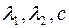эта кривая будет эллипсом, гиперболой, параболой, парой прямых, точкой или мнимой кривой.
