2020-05-12
112
Если функции 
и 
обладают непрерывными производными, то справедлива формула:
(3)
называемая формулой интегрирования по частям.
В качестве 
обычно выбирают функцию, которая упрощается при дифференцировании.
Некоторые стандартные случаи функций, интегрируемых по частям, указаны в табл. 1. Там же дается способ выбора множителей 
и 
.
Таблица 1
| Вид интеграла | 
| 
| |
| 
| 
| |
| 
|
| |
| 
| ||
| 
| ||
| 
| ||
| 
| ||
|
| |||
— многочлен от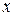 
степени 
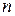, т. е. 
, где 
.
Пример. Проинтегрировать по частям.
Решение.
