1) подынтегральную функцию разложить в ряд Маклорена;
2) почленно проинтегрировать этот ряд, воспользовавшись формулой Ньютона-Лейбница;
3) в правой части оставить необходимое для обеспечения заданной точности число слагаемых, основываясь на следствии из признака Лейбница.
Пример 8. С точностью  вычислить определенный интеграл
вычислить определенный интеграл  .
.
Решение. Разлагая подынтегральную функцию в степенной ряд
согласно формуле
 ,
,
имеем

 .
.
Выполняя почленное интегрирование, получаем
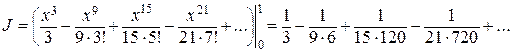 =
=

Получился сходящийся знакочередующийся ряд. Учитывая, что его четвертый член  , заключаем, что все члены ряда, начиная с четвертого, можно отбросить. Следовательно,
, заключаем, что все члены ряда, начиная с четвертого, можно отбросить. Следовательно,
 .
.
Округляя до четвертого знака после запятой, получаем
 .
.
Ряды Фурье
Пусть функция  задана на отрезке
задана на отрезке  и имеет период
и имеет период 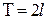 . Тригонометрическим рядом Фурье для функции
. Тригонометрическим рядом Фурье для функции 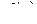 называется ряд вида:
называется ряд вида:
 , (1)
, (1)
а 0, аn, bn называются коэффициентами ряда и вычисляются по формулам
 ,
, 
 (2)
(2)
В тригонометрический ряд можно разложить функцию, удовлетворяющую определенным условиям, которые называются условиями Дирихле.
Функция 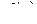 на отрезке
на отрезке  удовлетворяет условиям Дирихле, если
удовлетворяет условиям Дирихле, если
1) она непрерывна на этом отрезке или имеет на нем конечное число точек разрыва первого рода (т. е. в точках разрыва существуют конечные одно-сторонние пределы, но они не равны между собой);
2) функция на отрезке или не имеет точек экстремума, или имеет их конечное число;
3) существуют односторонние пределы 
 и
и  .
.
Сходимость тригонометрического ряда, составленного для функции f (x), определяется следующей теоремой.
Теорема Дирихле. Пусть функция  определена для
определена для 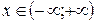 , имеет период
, имеет период 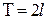 и на отрезке
и на отрезке  удовлетворяет условиям Дирихле. Тогда ее ряд Фурье сходится на всей числовой оси, т. е.
удовлетворяет условиям Дирихле. Тогда ее ряд Фурье сходится на всей числовой оси, т. е.
имеет сумму  .
.
При этом:
1) в точках непрерывности функции 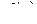 он сходится к самой функции, т. е.
он сходится к самой функции, т. е.  =
= 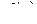 ;
;
2) в точках разрыва функции х 0 сумма ряда равна полусумме односторонних пределов функции слева и справа, т. е.  ;
;
3) на концах отрезка  сумма ряда определяется формулой:
сумма ряда определяется формулой:
 .
.
Для четной функции 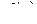 =
= 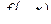 все коэффициенты bn =0, и ряд Фурье имеет вид:
все коэффициенты bn =0, и ряд Фурье имеет вид:
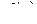
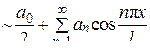 , (3)
, (3)
где  ,
,  n =1,2…,
n =1,2…,
т. е. четная функция разлагается в ряд Фурье только по косинусам.
Для нечетной функции 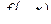 =
=  а 0=0, все a n=0. Тогда
а 0=0, все a n=0. Тогда
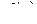
 ,
, 
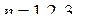 (4)
(4)
Таким образом, нечетная функция 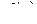 разлагается в ряд Фурье толь-ко по синусам. Функцию f (x), заданную на интервале (0, l), можно произ-вольно продолжить на интервал (–l, 0), или как четную, или как нечетную, а затем разложить в неполный ряд Фурье, содержащий только косинусы или только синусы.
разлагается в ряд Фурье толь-ко по синусам. Функцию f (x), заданную на интервале (0, l), можно произ-вольно продолжить на интервал (–l, 0), или как четную, или как нечетную, а затем разложить в неполный ряд Фурье, содержащий только косинусы или только синусы.
Алгоритм разложения функции 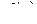 , заданной графически на интервале (0,l), в неполный ряд Фурье
, заданной графически на интервале (0,l), в неполный ряд Фурье
1) задать аналитически 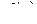 на (0, l);
на (0, l);
2) доопределить функцию на (–l, 0) четным или нечетным образом;
3) проверить выполнение условий Дирихле на (–l,l);
4) определить коэффициенты ряда Фурье для полученной функции и записать ряд Фурье;
5) определить сумму ряда  для
для 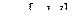 .
.
Пример 9. Функцию 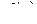 , заданную графически, разложить в ряд Фурье:
, заданную графически, разложить в ряд Фурье:


Рис. 1
Решение.
а) Функция, заданная графически (рис. 1, а), аналитически описывается следующим образом:
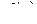 =
= 

Чтобы получить разложение данной функции в ряд Фурье, содержащий только косинусы, продолжаем ее на соседний слева интервал  четным образом (рис. 2).
четным образом (рис. 2).

Рис. 2
Полученная функция на  удовлетворяет условиям Дирихле: она имеет две точки разрыва первого рода x 1=-0,5 и x 2=0,5 и не имеет точек экстремума, поэтому ее можно разложить в сходящийся ряд Фурье. При этом bn =0, и по формуле (3), подставляя l =1, f (x)=0,3 в интервале (0; 0,5) и f (x)= – 0,3 в интервале (0,5; 1), найдем
удовлетворяет условиям Дирихле: она имеет две точки разрыва первого рода x 1=-0,5 и x 2=0,5 и не имеет точек экстремума, поэтому ее можно разложить в сходящийся ряд Фурье. При этом bn =0, и по формуле (3), подставляя l =1, f (x)=0,3 в интервале (0; 0,5) и f (x)= – 0,3 в интервале (0,5; 1), найдем
 =
=
=0,6 
 .
.
Использовали  ,
,  для
для 
Если п четное, т. е. п =2 k,  то
то  , т. е. a n=0 для четныхномеров n.
, т. е. a n=0 для четныхномеров n.
Если n нечетное, т. е. n = 2k−1,  то
то
 ,
,
т. к. по формулам приведения 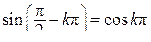 , а
, а 
 .
.
При п = 0 по формуле для а 0 получим:
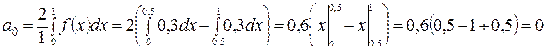 .
.
Следовательно, искомое разложение данной функции в неполный ряд Фурье, содержащий только косинусы, следующее:

По теореме Дирихле полученный ряд сходится на всей числовой оси, При этом для суммы этого ряда S (x) выполняется
1. S (x) = f (x) во всех точках непрерывности функции f (x), т. е. при  , и в разложении функции знак ~ можно заменить на знак =.
, и в разложении функции знак ~ можно заменить на знак =.
2. Определим S (x) в точках разрыва х 1= – 0,5, х 2= 0,5. 
 ,
,
 .
.
3. На концах интервала, в точках x = –l и x = l, l = 1 имеем

б) Функция, заданная графически (рис. 1, б), аналитически описывается следующим образом:

Чтобы получить разложение данной функции в ряд Фурье, содержащий только синусы, продолжим ее на  нечетным образом (рис 3).
нечетным образом (рис 3).

Рис. 3
Полученная функция на  удовлетворяет условиям Дирихле: имеет две точки разрыва первого рода х 1
удовлетворяет условиям Дирихле: имеет две точки разрыва первого рода х 1  , х 2
, х 2  и не имеет точек экстремума, поэтому ее можно разложить в ряд Фурье, сходящийся на всей числовой оси.
и не имеет точек экстремума, поэтому ее можно разложить в ряд Фурье, сходящийся на всей числовой оси.
Функция нечетная, поэтому ап = 0, п = 0,1,2,…; bn вычислим по форму-ле (4), подставляя  ,
,  в интервале
в интервале  и
и  в интервале
в интервале  :
:

 ,
,
п = 1,2,3,….
Следовательно, ряд Фурье для функции имеет вид:
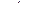 ~
~ 
= 
По теореме Дирихле полученный ряд сходится на всей числовой оси и имеет сумму S (x). При этом:
1. S (x)= f (x) для  и в разложении знак ~ можно заменить на знак =.
и в разложении знак ~ можно заменить на знак =.
2. В точках разрыва х 1=  и х 2=
и х 2=  сумма ряда равна:
сумма ряда равна:
 ,
,
 .
.
3. На концах интервала в точках  ,
,  имеем
имеем

ПРИЛОЖЕНИЕ I
Таблица основных интегралов
1.  2.
2. 
3. 

4.  5.
5. 
6.  7.
7. 
8.  9.
9. 
10.  11.
11. 
12.  13.
13. 
14.  15.
15. 
16. 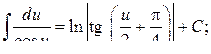 17.
17. 
18. 
ПРИЛОЖЕНИЕ II
 2020-05-12
2020-05-12 114
114








