Для того чтобы выполнить это задание, необходимо вспомнить некоторые понятия из темы «Аналитическая геометрия в пространстве». Ненулевой вектор параллельный прямой называется направляющим вектором прямой. Два вида уравнений прямой в пространстве:
– канонические: 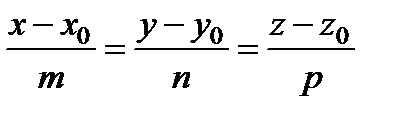 ,
,
где 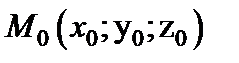 — фиксированная точка, лежащая на прямой
— фиксированная точка, лежащая на прямой 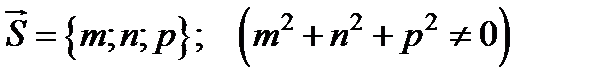 — направляющий вектор прямой;
— направляющий вектор прямой;
– параметрические: 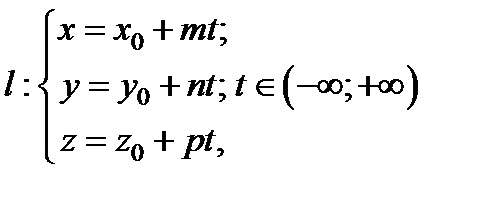
(между точками прямой и значениями параметра 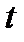 установлено взаимно однозначное соответствие). Если в параметрических уравнениях исключить параметр
установлено взаимно однозначное соответствие). Если в параметрических уравнениях исключить параметр 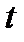 , то получим канонические уравнения.
, то получим канонические уравнения.
Нахождение уравнения плоскости, проходящей через заданную точку и заданную прямую, заключается в нахождении координат двух различных точек, лежащих на заданной прямой. Нужно составить уравнение плоскости, проходящей через прямую 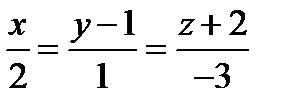 и точку
и точку 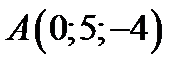 .
.
Сначала напишем общее уравнение плоскости. Общее уравнение плоскости — всякое уравнение вида 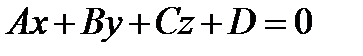 , где
, где 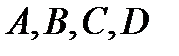 — некоторые действительные числа, причем
— некоторые действительные числа, причем 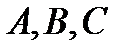 одновременно не равны нулю.
одновременно не равны нулю.
Для этого найдем координаты двух различных точек, лежащих на прямой 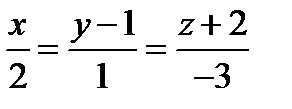 .
.
Параметрические уравнения этой прямой имеют вид: 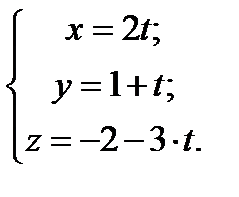
Пусть точка 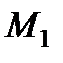 соответствует значению
соответствует значению 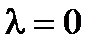 , а точка
, а точка 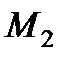 соответствует
соответствует 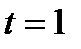 . Вычисляем координаты точек
. Вычисляем координаты точек 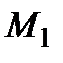 и
и 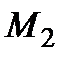 :
:
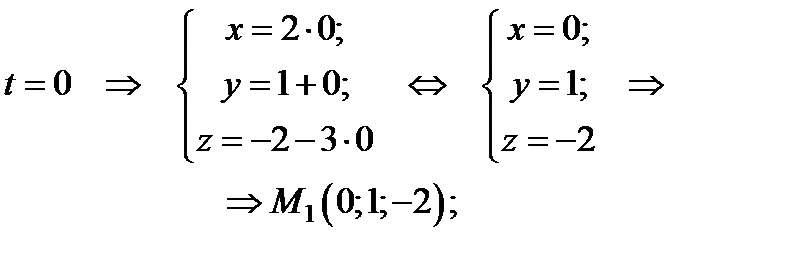
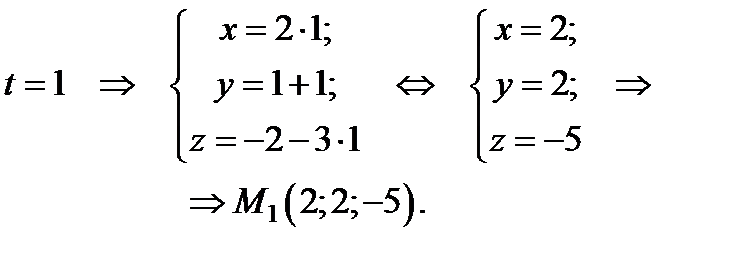
Теперь мы можем составить общее уравнение прямой, проходящей через точку 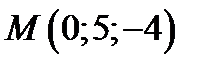 и прямую
и прямую 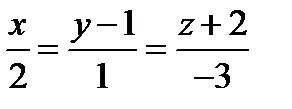 .
.
Используем формулу плоскости, проходящей через три точки 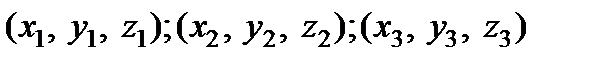
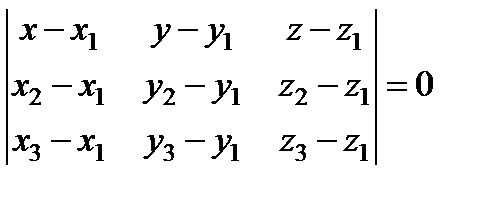 .
.
В нашем случае это:
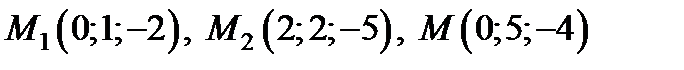 .
.
Имеем:
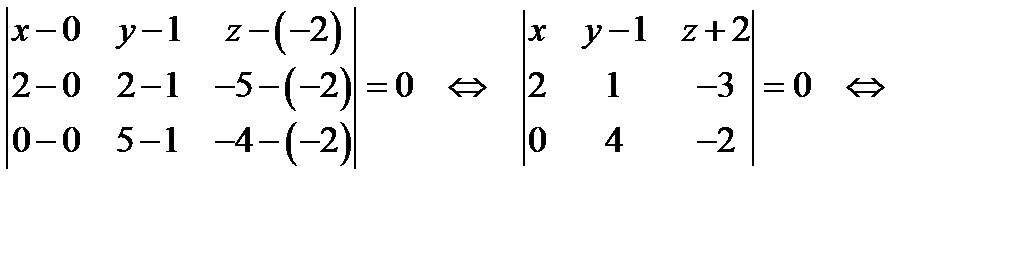
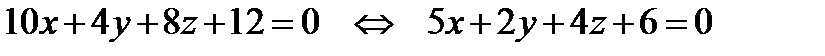 .
.
Задача 2
Найти косинус угла между плоскостями 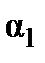 и
и 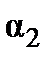 .
.
Вспомним некоторые теоретические моменты. Пусть плоскости 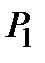 и
и 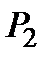 заданы уравнениями:
заданы уравнениями:
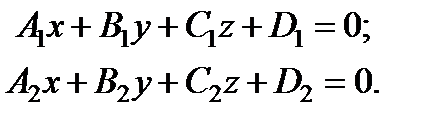
Нормальные векторы, определяющие эти плоскости, задаются координатами:
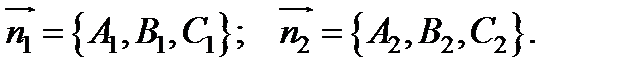
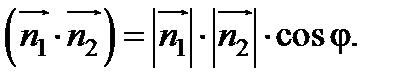
Один из двугранных углов между плоскостями равен острому углу между их нормальными векторами и определяется из равенства:
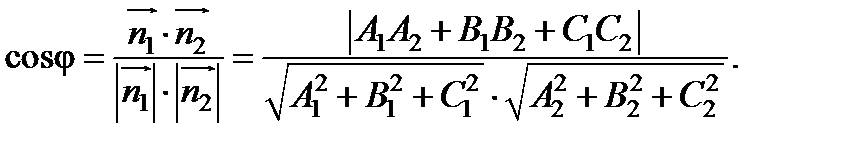
Рассмотрим типовое задание: пусть даны уравнения плоскостей 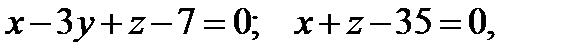 тогда
тогда
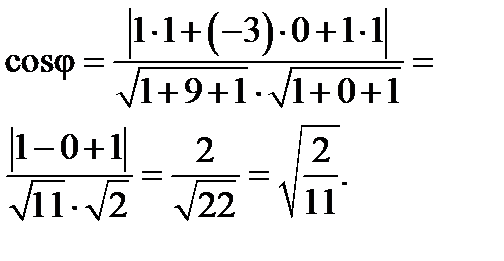
 2020-05-21
2020-05-21 2833
2833
