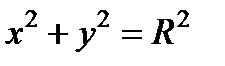Каноническое уравнение окружности

,

где — радиус окружности.

Каноническое уравнение эллипса

,

где  — большая, — малая полуоси эллипса .

Каноническое уравнение гиперболы

,

где — действительная полуось,  — мнимая полуось.

Каноническое уравнение параболы, симметричной относительно оси  

;  — действительное число.

Каноническое уравнение параболы, симметричной относительно оси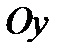

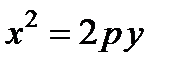;  — действительное число.

Любая кривая второго порядка представляет собой одну из канонических кривых (эллипс, гиперболу или параболу). Путем преобразования системы координат (параллельного переноса) приведем заданное уравнение к каноническому уравнению, описывающему одну из этих кривых.

При параллельном переносе осей координат используем формулы перехода от системы координат 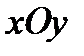 к новой системе координат :

где 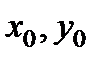 — координаты точки .

Выясним, какую кривую второго порядка описывает уравнение

.

Сгруппируем переменные для того, чтобы выделить полный квадрат:

.

Отсюда

.

Дополним выражения, стоящие в скобках, до полного квадрата

.

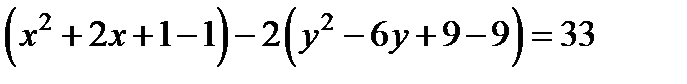Отсюда

;

или .

Разделим обе части уравнения на 16, чтобы получить 1 в правой части:

.

Получаем

.

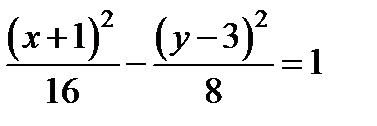Точка  — начало новой системы координат — совпадает с центром кривой второго порядка. Применим формулу для  и , получим каноническое уравнение гиперболы с полуосями , . В результате имеем

.

Построим данную кривую. Эта кривая — смещенная гипербола. Она изображена на рисунке:

 

 

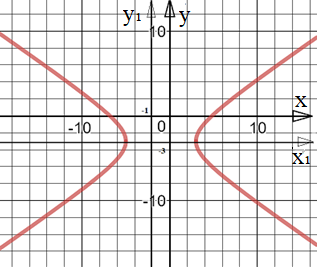
4.3 Прямая в пространстве. Плоскости

Задача 1