Функции нескольких переменных

Цель раздела: изучить теоретический материал раздела на примере функций двух переменных, научиться решать стандартные задачи тем «Дифференциальное исчисление функций двух переменных», «Исследование на экстремум функций двух переменных», «Нахождение наибольшего и наименьшего значений функций двух переменных», «Градиент и производная по направлению».

5.1 Дифференциальное исчисление функций двух переменных

Определение 1. Говорят, что в области 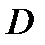 плоскости  задана функция двухпеременных , если каждой точке  ставится в соответствие по некоторому правилу  единственное значение переменной величины .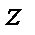

В этом случае 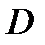 называется областью определения функции .

Пусть  некоторая произвольная фиксированная точа из области определения функции . Придавая переменной 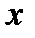 приращение , находим приращение функции  в точке  по переменной :

Определение 2. Частнойпроизводной первого порядка функции  в точке 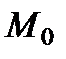 по переменной  называется предел отношения частного приращения  в этой точке к вызвавшему его приращению  переменной  при .

Обозначения:

 

Итак, согласно определению,

.           

Аналогично

.     

— частная производная по переменной .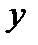

Ø Из приведенных определений легко получить правило нахождения частных производных функции нескольких переменных:

 

При вычислении частной производной по одной из независимых переменных все остальные независимые переменные считают постоянными величинами и применяют правила дифференцирования функции одной переменной.

 

Определение 3. Полныйдифференциал  дифференцируемой функции 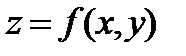 есть выражение вида

                                   

Определение 4. Частными производными второго порядка от функции 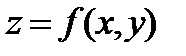 называют частные производные от ее частных производных первого порядка

, , ,   .

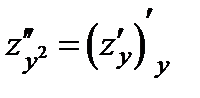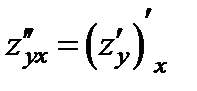Две последние производные принято называть смешанными.

Смешанные производные, отличающиеся друг от друга лишь последовательностью дифференцирования, равны между собой, если они непрерывны.

.                                                 

 

Пример 1. Найти частные производные функции: .

       Решение:

(производная второго слагаемого равна нулю как производная константы)

.

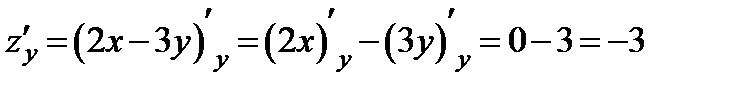Пример 2. Найти частные производные функции: .

       Решение:

  .

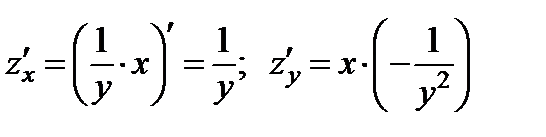Пример 3. Найти частные производные функции: .

 

       Решение:

Частная производная по переменной  является производной степенной функции с фиксированным показателем ; поэтому .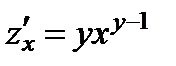

Частная производная по переменной  является производной показательной функции с фиксированным основанием 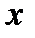; поэтому .

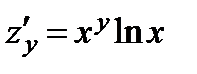Пример 4. Найти частные производные функции:

.

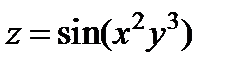       Решение:

По правилу дифференцирования сложной функции:

;

.

 

Пример 5. Найти полный дифференциал функции:

Решение:

Найдем производные первого порядка. Вычисляя производную по , полагаем  постоянным:

 

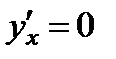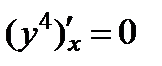так как  и , то

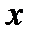Аналогично, вычисляя производную по , полагаем  постоянным:

так как 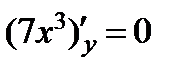 и , то

.

Выпишем получившиеся производные:

,

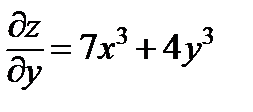
Подставим их в формулу полного дифференциала (3), получаем:

 

Пример 6. Найти частные производные второго порядка функции: .

Решение:

Частные производные первого порядка имеют вид

, .

Считая их новыми функциями двух переменных, найдем их частные производные. Получаем:

,

,

.

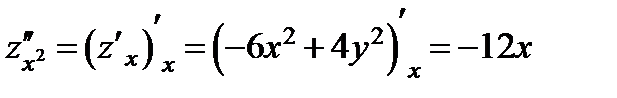Ø Обратите внимание! Мы нашли только три частные производные второго порядка, так как смешанные производные равны между собой, если они непрерывны.

Проверим это утверждение на нашем примере. Функция и все ее производные непрерывны на . Найдем вторую смешанную производную:

Мы получили .

 

5.2 Экстремум функции 2-х переменных

Пусть функция  задана в области , содержащей точку .

 внутренняя точка области

  Определение 1. Точка 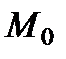 называется точкоймаксимума  функции , если для всех точек  из некоторой окрестности точки  выполняется неравенство .

Определение 2. Аналогично точка  называется точкойминимума функции , если для всех точек 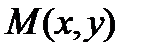 из некоторой окрестности точки  выполняется неравенство .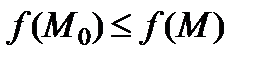

Определение 3. Точки максимума и минимума называют точкамиэкстремума.

 

Определение 4. Стационарными точками функции называются точки, лежащих внутри области определения функции, в которых все ее частные производные первого порядка равны нулю или не существуют.

Функция многих переменных может иметь максимум или минимум (экстремум) только в стационарных точках.

 

Теорема 1. ( Необходимое условие экстремума)

Если в точке экстремума  обе частные производные функции  существуют и непрерывны, то они равны нулю в этой точке:

;

.

 

Теорема 2. (Достаточное условие экстремума)

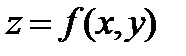Пусть в окрестности точки стационарной  функция  имеет непрерывные частные производные до второго порядка включительно.

 

Обозначим:

; ; ;

 

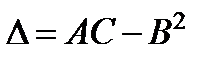
Тогда:

· если 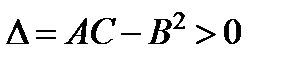, то в точке  есть

экстремум;

1) при  функция  в точке  имеет максимум;

2) при  функция  в точке  имеет минимум.

· если , то экстремума заведомо нет;

· если , то заключение о наличии экстремума сделать нельзя, требуется дополнительное исследование.

 

Пример 7. Исследовать функцию на экстремум:

 .

Решение:

Найдем частные производные первого порядка:

;

.

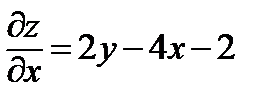Приравняем нулю эти выражения и решим получившуюся систему относительно 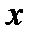и . В результате:

Решая систему, найдем координаты стационарнойточки. Такой точкой является точка 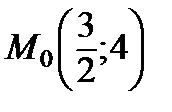. Экстремума в этой точке может и не быть.

 Наличие экстремума в точках устанавливается с помощью производных второго порядка.

                 

Т.к. , следовательно, экстремум есть.

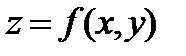Поскольку величина , то в точке  функция  имеет максимум. Вычислим значение функции в найденной точке:

.

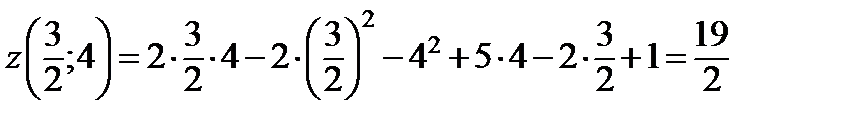Таким образом, данная функция имеет один экстремум в точке . Это максимум, значение которого равно .

5.3 Наибольшее и наименьшее значения функции

Пусть функция  определена и непрерывна в некоторой ограниченной и замкнутой области .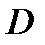

Чтобы найти наибольшее (наименьшее) значение функции

в ограниченной замкнутой области , где она непрерывна, можно руководствоваться следующим правилом:

5 Найти стационарныеточки, лежащие внутри области 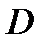, и вычислить значения функции в этих точках (не вдаваясь в исследование, будет ли в них экстремум и какого вида).

6 Найти наибольшее (наименьшее) значение функции на границе области .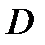

7 Сравнить полученные значения функции: самое большее (меньшее) из них и будет наибольшим (наименьшим) значением функции во всей области .

 

Пример 8. Найти наименьшее и наибольшее значения функции   в треугольнике, ограниченном данными прямыми:

,

 

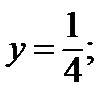
Решение:

Сделаем чертеж области. Прямая  вертикальна и совпадает с осью ординат. Прямая  горизонтальна и параллельна оси абсцисс. Прямая 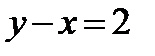 наклонна и проходит под углом  через точку . Точка пересечения прямых первой и второй есть .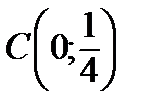

Координаты точки пересечения прямых второй и третьей найдутся в результате решения системы, составленной из уравнений этих прямых:

Имеем точку пересечения .

Чертеж области представлен на рисунке 1.

 

                             

Рис. 1

 

Наибольшее и наименьшее значение в замкнутой области функция может принимать, либо в точках экстремума внутри области, либо на границе области.

1. Вычислим первые частные производные и найдем точки, подозрительные на экстремум.

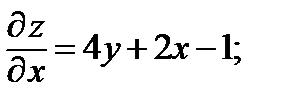
Найдена одна точка. Она лежит внутри области. Найдем значение функции в этой точке.

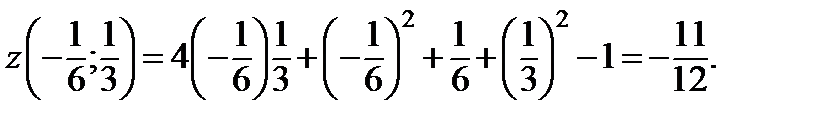
2. Исследуем функцию вдоль каждой из трех границ.

На каждом из граничных отрезков функция  оказывается функцией одного аргумента.

Наибольшее и наименьшее значения принимаются либо внутри, либо на концах отрезков.

Рассмотрим первую границу :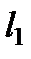  

Найдем выражение функции  вдоль этой границы. Подставим  в выражение для .

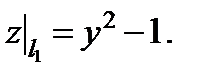
Имеем функцию одной переменной . Найдем ее производную и приравняем нулю.

Откуда получаем  Это значение не принадлежит промежутку .

Вдоль этой границы наибольшее и наименьшее значения могут приниматься лишь на концах промежутка.

Найдем значения функции в этих точках:

 

      .

Рассмотрим вторую границу :

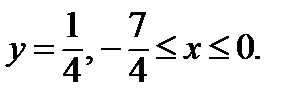
Вдоль этой границы  принимает следующие значения:

Найдем производную и приравняем нулю 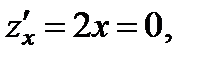 откуда

 Это значение не является внутренним для промежутка . Найдем значение функции на концах промежутка

Значение функции в точке  уже найдено в предыдущем пункте.

Рассмотрим третью границу : .

Это уравнение можно представить в виде  где

Подставим это выражение для  в правую часть :

Найдем производную и приравняем ее нулю

Откуда получаем  Это значение лежит внутри промежутка

Найдем значение функции в этой точке:

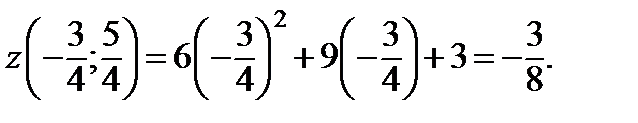
Точки концов промежутка  соответствуют уже рассмотренным точкам вершин треугольника

.

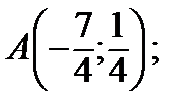
 Значения функции в этих точках уже найдены.

       Составим сравнительную таблицу, куда занесем координаты точек 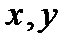 и соответствующие значения .

 

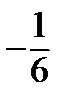
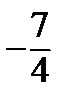
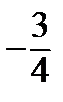
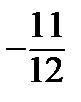
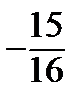
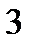
По нижней строчке таблицы находим наибольшее и наименьшее значения.

Наибольшим является

Наименьшим является

 

5.4 Градиент и производная по направлению

Определение 1. Градиентом функции  в точке 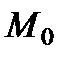 называется вектор, координатами которого являются значения частных производных в этой точке.

Обозначения: .

                        

Градиент функции в точке  задает направление наибольшей скорости изменения функции в малой окрестности этой точки.

Определение 2. Производной по направлению называется скорость изменения функции в точке  в направлении вектора . Если найден градиент функции в точке , то производную по направлению вектора  можно найти по формуле

                                             

Пример 9. Даны функция , точка   и вектор .

Найти градиент функции 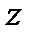  в точке   и производную от функции в точке 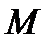  по направлению вектора :

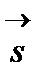Решение:

Найдем градиент функции как вектор, координатами которого в ортонормированном базисе , являются значения частных производных в точке М (формула (5)).

Предварительно вычислим частные производные

 

Производные функции в точке  принимают значения:

     

Вектор  в этой точке имеет вид:

Производную по направлению находим по формуле (6), где точка – это знак скалярного произведения векторов.

Найдем модуль вектора :

Скалярное произведение находим как сумму попарных произведений координат векторов множителей , :

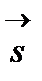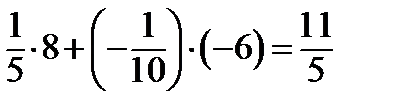, тогда

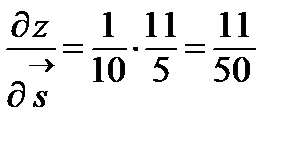
Искомое значение производной по направлению равно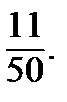

5.5 Контрольные вопросы по разделу «Функции нескольких переменных»

1. Предел функции двух переменных. Приращения функции двух переменных. Определение и критерий непрерывности.

2. Частные производные; геометрический смысл; вычисление.

3. Определение дифференцируемости; теорема о коэффициентах; полный дифференциал.

4. Формула для полного приращения. Достаточное условие дифференцируемости.

5. Частные производные сложной функции. Полная производная сложной функции.

6. Частные производные высших порядков. Теорема о смешанных производных.

7.  Необходимое условие экстремума. Достаточное условие экстремума.

8. Производная по направлению: определение; вывод формулы.

9. Градиент; связь производной по направлению с градиентом.

 

5.6 Задачи для проведения промежуточного контроля усвоения материала раздела «Функции нескольких переменных»

     Задание 1. Найти частные производные второго порядка .

1.		2.
3.		4.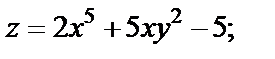
5.		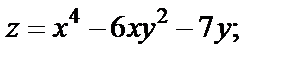6.
7.		8.
9.		10.

Задание 2

  1. Дана функция .Показать, что

  2. Дана функция . Показать, что .

  3. Дана функция . Показать, что .

  4. Дана функция . Показать, что

  5. Дана функция. Показать, что

  6. Дана функция. Показать, что

  7. Дана функция .Показать, что

  8. Дана функция. Показать, что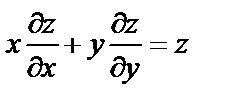

  9. Дана функция. Показать, что .,,

10. Дана функция. 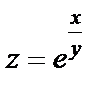Показать, что

Задание 3. Исследовать функцию на экстремум.

1.
2.
3.
4.
5.
6.
7.
8.
9.
10.

8 ЗАКЛЮЧЕНИЕ

Электронное учебное пособие по дисциплине «Математика» разработано в соответствии с федеральным государственным образовательным стандартом по уровню специалитета.

В электронном учебном пособии содержится материал для самостоятельной работы обучающихся по разделам и темам 2 семестра 1 курса. В пособие включены следующие разделы:

 

1. Неопределенные интегралы,

2. Определенные интегралы,

3. Несобственные интегралы.

4. Аналитическая геометрия

5. Дифференциальное исчисление функций нескольких переменных

 

Содержание данного электронного учебного пособия соответствует рабочей программе дисциплины и основано на материалах отечественных и зарубежных исследований, включая современные публикации.

Рабочей программой дисциплины «Математика» предусмотрено формирование следующих компетенций, выполнение которых фиксируется с помощью следующих индикаторов

Код и наименование компетенции	Код и наименование индикатора достижения компетенции	Планируемые результаты обучения по дисциплине
ОПК-2. Способен применять естественнонаучные и общеинженерные знания, аналитические методы в профессиональной деятельности	ОПК-2.1. Знает основные законы естественнонаучных дисциплин, связанные с профессиональной деятельностью	Знает методы математического анализа, линейной алгебры, теории дифференциальных уравнений; основные понятия и методы векторной алгебры; основы операционного исчисления
	ОПК-2.2. Умеет применять основные законы естественнонаучных дисциплин в профессиональной деятельности	Умеет применять математические методы при решении типовых профессиональных задач
	ОПК-2.3. Владеет навыками применения основных законов естественнонаучных дисциплин в профессиональной деятельности	Владеет математическим аппаратом для решения практических задач
ОПК-3. Способен проводить измерения и наблюдения, обрабатывать и представлять экспериментальные данные	ОПК-3.1. Знает способы измерений, записи и хранения результатов наблюдений, методы обработки и представления экспериментальных данных	Знает основные понятия, определения, методы теории вероятностей и математической статистики и их применение для обработки и представления данных
	ОПК-3.2. Умеет обрабатывать экспериментальные данные, интерпретировать и профессионально представлять полученные результаты	Умеет логически мыслить, устанавливать логические связи между полученными экспериментальными данными.
	ОПК-3.3. Владеет навыками работы с измерительными приборами и инструментами	Владеет методами содержательной интерпретации полученных результатов, методами проведения измерений и корректной оценки погрешностей