Ряд распределений дискретной случайной величины и его свойство

Ряд распред- табл, где перечислены все значения и указаны их вер-ти.

Закон распределения дискр случ величины обычно задается рядом распределения.

X итое  x1 x2 … x_n

P итое  р1 р2 … pn (только это еще в табличке). При этом

n

∑рi = 1, где суммирование распространяется на все (конечное или бескон) множество

I=1

значений данной случайной величины Х.

 

С

. Сформулируйте условие, при котором для вычисления вероятности 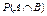 следует применять теорему умножения для зависимых событий. Приведите формулировку этой теоремы.

При условии того, что из одного события «вытекает» другое.

Вероятность совместного появления двух событий равно произведению вероятности одного из них на условную вероятность другого, вычисленную в предположении, что первое событие уже наступило P(AC) = P(A)*P(C/A).

. Сформулируйте условие, при выполнении которого можно утверждать, что событие  не зависит от события ?

если условная вероятность события В равно его безусловной вероятности: Ра(В)=Р(В)

 

. Сформулируйте условие, при выполнении которого можно утверждать, что событие 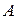 зависит от события ?

два события называются зависимыми, если вероятность их совмещения не равна произведению вероятности этих событий!

 

Сформулируйте условие, при выполнении которого можно утверждать, что событие В зависит от события А.

Два события называются зависимыми, если вероятность их совмещения не равна произведению вероятности этих событий!

. Сформулируйте условия, при выполнении которых можно утверждать, что гипотезы Н₁, Н₂, Н_n образуют полную группу событий.

Говорят, что события H 1, H 2, …, Hn образуют полную группу, если они попарно несовместны (H_i ∩ H_j = ∅, i ≠ j), и их объединение эквивалентно достоверному событию (H ₁ ∪ H ₂ ∪ ··· ∪ H_n = Ω).

Сформулируйте условия, при выполнении которых можно для вычисления вероятности некоторого события А можно использовать формулу полной вероятности. Приведите формулировку и краткое доказательство формулы полной вероятности.

Если события H1, H2, …, Hn ∈ S образуют полную группу и имеют положительные вероятности, то для любого события A ∈ S

                                                                                            n

P(A)=P(A│H₁)P(H₁)+P(A│H₂)P(H₂)+…+P(A│H_n)P(H_n)= ∑P(A│H_i)P(H_i).

                                                                                           i=1

В соответствии с этой формулой вероятность наступления события A может быть представлена как сумма произведений условных вероятностей события A при условии наступления событий Hi на безусловные вероятности этих событий Hi. Поскольку среди событий H 1, H 2, …, Hn, образующих полную группу, в результате опыта должно наступить одно и только одно, эти события Hi называют гипотезами (i = 1, 2, …, n).

Доказательство. Очевидно, A = (A ∩ H 1)∪(A ∩ H 2)∪ · · · ∪(A ∩ Hn), причем события (A ∩ H 1), (A ∩ H 2), …, (A ∩ Hn) несовместны (поскольку несовместны события H 1, H 2, …, Hn). По аксиоме аддитивности вероятности P(A) = P(A ∩ H 1) + P(A ∩ | H 2)P(H 2) + ··· + P(A ∩ Hn). Каждую из вероятностей P(A ∩ Hi) раскроем по формуле умножения вероятностей: P(A ∩ Hi) = P(A | Hi)P(Hi) (i = 1, 2, …, n). Подставляя, получаем: P(A) = P(A | H 1)P(H 1) + P(A | H 2)P(H 2) + · · + P(A | Hn)P(Hn), что и требовалось доказать. 􀂉

Формула полной вероятности остается справедливой и в случае, если условие, состоящее в том, что события H 1, H 2, …, Hn образуют полную группу, заменить более слабым: гипотезы H 1, H 2, …, Hn попарно несовместны (Hi ∩ Hj = ∅ при i ≠ j), а событие A влечет за собой объединение этих гипотез (A ⊆ H 1∪ H 2∪ ··· ∪ Hn).