Пусть функция 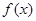 определена во всех точках интервала (a, b), за исключением, быть может, точки
определена во всех точках интервала (a, b), за исключением, быть может, точки 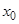 . Возьмем последовательность точек
. Возьмем последовательность точек 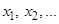 , принадлежащих интервалу (a, b) и отличных от точки
, принадлежащих интервалу (a, b) и отличных от точки 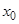 . Предположим, что { xn } сходится к
. Предположим, что { xn } сходится к 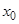 , т.е.
, т.е.  . Тогда значения функции
. Тогда значения функции 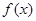 также образуют числовую последовательность
также образуют числовую последовательность 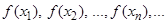 .
.
Определение 1. Число 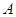 называют пределом функции
называют пределом функции 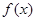 в точке
в точке 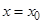 (или при
(или при 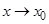 ) и пишут
) и пишут 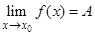 , если для любой последовательности значений аргумента{ xn }, сходящейся к
, если для любой последовательности значений аргумента{ xn }, сходящейся к 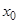 , причем
, причем 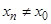 , последовательность значений функции
, последовательность значений функции 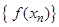 сходится к числу
сходится к числу 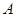 .
.
Определение 2 (эквивалентное первому). Число 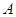 называют пределом функции f (x) при x, стремящемся к x 0, и пишут
называют пределом функции f (x) при x, стремящемся к x 0, и пишут 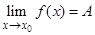 , если для любого наперед заданного сколь угодно малого числа
, если для любого наперед заданного сколь угодно малого числа 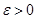 можно указать такое число
можно указать такое число 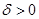 , зависящее от e, что при всех
, зависящее от e, что при всех 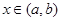 и
и 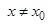 , удовлетворяющих неравенству
, удовлетворяющих неравенству 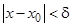 , выполняется неравенство
, выполняется неравенство 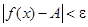 .
.
Пусть функция 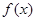 определена на промежутке
определена на промежутке 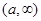 . Число
. Число 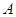 называется пределом функции
называется пределом функции 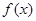 при
при 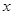 стремящемся к
стремящемся к 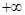 , т.е.
, т.е. 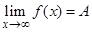 , если для любого числа
, если для любого числа 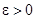 можно указать такое число
можно указать такое число 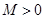 , зависящее от e, что при всех x, удовлетворяющих неравенству
, зависящее от e, что при всех x, удовлетворяющих неравенству 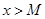 , выполняется неравенство
, выполняется неравенство 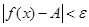 .
.
 2020-05-25
2020-05-25 140
140








