Определение последовательности и ее предела

Переменная величина , последовательные значения которой можно пронумеровать , называется числовой последовательностью { x_n }.

Последовательность { x_n } называется возрастающей, если x_n < x_n ₊₁ для всех натуральных значений индекса ; неубывающей, если x_n £ x_n ₊₁; убывающей, если x_n > x_n ₊₁, и невозрастающей, если x_n ³ x_n ₊₁ для всех значений индекса . Все такие последовательности называются монотонными. Возрастающие и убывающие последовательности называются также строго монотонными.

Последовательность { x_n } называется ограниченной сверху (или снизу ), если существует число M (или ) такое, что при всех натуральных n выполняется неравенство 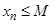(или ). Последовательность { x_n } называется ограниченной, если она ограничена и сверху, и снизу.

Число a называют пределом последовательности { x_n } и пишут (или при ), если для любого сколь угодно малого положительного числа найдется такой номер N, что при всех n > N выполняется неравенство .

Интервал (a – e, a + e) называется e- окрестностью точки a.

Последовательность, имеющая предел, называется сходящейся, последовательность, не имеющая предела, — расходящейся.

1.2.2 Свойства бесконечно малых и бесконечно больших величин

Последовательность a _n называется бесконечно малой, если для любого сколь угодно малого положительного числа e существует номер N такой, что при всех n > N выполняется неравенство |a _n | < e. Предел бесконечно малой величины равен нулю:

Последовательность 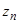называется бесконечно большой, если для любого положительного числа M существует номер N такой, что при всех n > N выполняется неравенство | z_n | > M. В этом случае пишут или .

Теорема: последовательность, обратная бесконечно большой, является бесконечно малой, т.е. если , то .

Теорема: последовательность, обратная бесконечно малой, является бесконечно большой, т.е. если 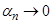, то .

Теорема: произведение бесконечно малой последовательности на ограниченную последовательность есть бесконечно малая последовательность.

Теорема: сумма бесконечно большой последовательности и ограниченной последовательности есть бесконечно большая последовательность.

1.2.3 Свойствасходящихся последовательностей

Теорема (о единственности предела): если последовательность сходится, то она имеет только один предел.

Теорема (об ограниченности сходящейся последовательности): если последовательность сходится, то она ограничена.

Ограниченность является необходимым, но не является достаточным условием сходимости, ограниченная немонотонная последовательность может предела не иметь.

Теорема (о пределе суммы, произведения и частного): если последовательности { x_n } и { y_n } сходятся, то их сумма, разность и произведение суть сходящиеся последовательности.

При этом

В частности, если — постоянная величина, то

При дополнительном условии: для любого и частное двух сходящихся последовательностей есть сходящаяся последовательность.

При этом

Теорема (о предельном переходе в неравенстве): если элементы сходящейся последовательности { x_n }, начиная с некоторого номера, удовлетворяют неравенству

x_n ³ b (или x_n £ b) то и предел этой последовательности удовлетворяет неравенству

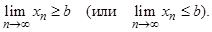
Теорема (о сжатой последовательности): если даны три последовательности { x_n },{ y_n } и { z_n }, причем 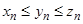для всех n, и последовательности { x_n } и { z_n } имеют один и тот же предел a, то последовательность { y_n } также имеет предел a.