2020-05-25
142
· Если кривая 
на отрезке 
– гладкая (т.е. производная 
непрерывна), то длина дуги этой кривой, содержащейся между двумя точкам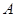и 
и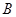 
с абсциссами 
и 
, равна
. 
· Если кривая задана уравнениями в параметрической форме 
и 
, где и непрерывно дифференцируемые функции, то длина дуги кривой равна
,
где 
и 
– значения параметра, соответствующие концам дуги.
Пример 7. Определить длину окружности 
Решение: Уравнение 
определяет окружность радиуса 
с центром в начале координат (рис. 9). 
Рис. 9
Вычислим сначала длину четверти окружности, лежащей в первом квадранте – это дуга 
. Тогда уравнение дуги будет: 
. Дифференцируя это уравнение, найдем:
. Тогда по формуле
= 
= 
.
Длина всей окружности равна 
.
Вычисление объема тела вращения.
· Объем тела, образованного вращением криволинейной трапеции, ограниченной кривой 
, осью 
и двумя вертикалями и 
, вокруг оси , находится по формуле:
|
|
|
Если фигура, ограниченная кривыми 
, 
и прямыми , , вращается вокруг оси , то объем тела вращения находится по формуле:
Пример 8. Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной кривыми 
, 
и осью 
.
Решение: Найдем точки пересечения кривых 
и . Имеем:
. 
Þ 
, 
.
Так как по условию 
, – посторонний корень.
Кривые пересекаются только в одной точке с координатами 
(рис. 11)
Объем тела вращения (рис.14), образованного вращением криволинейного треугольника 
,состоит из суммы объемов тел вращения
, где
– объем тела вращения, образованного вращением криволинейного треугольника 
,
– объем тела вращения, образованного вращением криволинейного треугольника 
По формуле (36) находим:
= 
(куб.ед.).
Рис. 11
Чтобы найти 
, преобразуем уравнение кривой : 
.
Тогда по формуле находим:
= 
(куб.ед.).
Следовательно,
+ 
(куб.ед.).
Если изобразить данное тело вращения, то получится фигура следующего
вида:
Рис. 12
