2020-05-21
465
Гармонические колебания происходят в замкнутой механической системе (
= 0) под действием упругой (квазиупругой) силы, в отсутствие сил трения (сопротивления). Полная механическая энергия системы при этом сохраняется.
Согласно II закону Ньютона,
,
Учитывая, что 
и вводя обозначение 
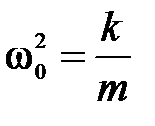, получим
. (2.2)
Это дифференциальное уравнение свободных незатухающих колебаний.
Решениями этого дифференциального уравнения являются функции:
, (2.3)
где 
– смещение от положения равновесия в момент времени 
; 
–амплитуда колебаний, т. е. максимальное смещение (взятое по модулю) от положения равновесия; 
– циклическая частота незатухающих колебаний – скалярная физическая величина, численно равная числу полных колебаний, совершенных за 
секунд; 
– начальная фаза колебаний – определяет фазу колебаний в начальный момент времени;. 
– фаза колебаний – величина, определяющая смещение от положения равновесия в данный момент времени.
Кроме того, к основным характеристикам колебаний относятся также следующие величины: 
– период незатухающих колебаний, т. е. промежуток времени, за которое совершается одно полное колебание; 
– частота колебаний, численно равная числу полных колебаний, совершенных системой за 1 секунду.
, (2.4)
. (2.5)
В случае пружинного маятника циклическая частота и период незатухающих колебаний равны соответственно:
, (2.6)
а для математического маятника, с учетом того, что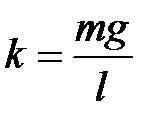 
:
, (2.7)
Рассмотрим, как изменяются со временем скорость и ускорение колеблющегося тела. Пусть смещение тела от положения равновесия изменяется по закону косинуса:
. (2.8)
Учитывая определения скорости и ускорения тела, запишем:
, (2.9)
, (2.10)
где 
и 
– амплитудные (максимальные) значения скорости и ускорения колеблющегося тела, соответственно.
Графики зависимостей (2.8) – (2.10) при 
представлены на рис. 2.3
Рис. 2.3
Тело, совершающее гармонические колебания, обладает и кинетической, и потенциальной энергией:
(2.11)
. (2.12)
Поскольку в системе нет неконсервативных сил, то полная механическая энергия W системы не изменяется:
. (2.13)
На рис. 2.4 приведены графики зависимости кинетической, потенциальной энергии системы, отвечающие зависимостям (2.11), (2.12) при , а также полной энергии.
Как видно из графиков, приведенных на рис. 2.3 и 2.4, период изменения потенциальной и кинетической энергий в два раза меньше, чем для смещения х.
Рис. 2.4
Затухающие колебания
