Пусть на тройке 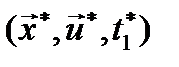 достигается минимум функционала (
достигается минимум функционала (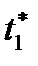 - если не задано t 1)
- если не задано t 1)
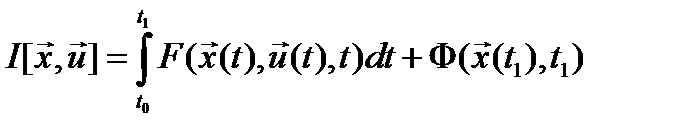 ,
,
тогда существует такая вектор-функция 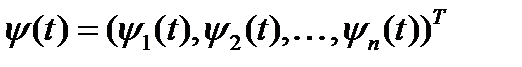 , что:
, что:
1). В каждой точке оптимального управления 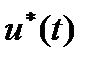 функционал
функционал 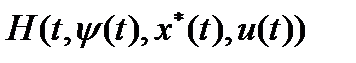 достигает максимума по управлению, т.е.
достигает максимума по управлению, т.е.
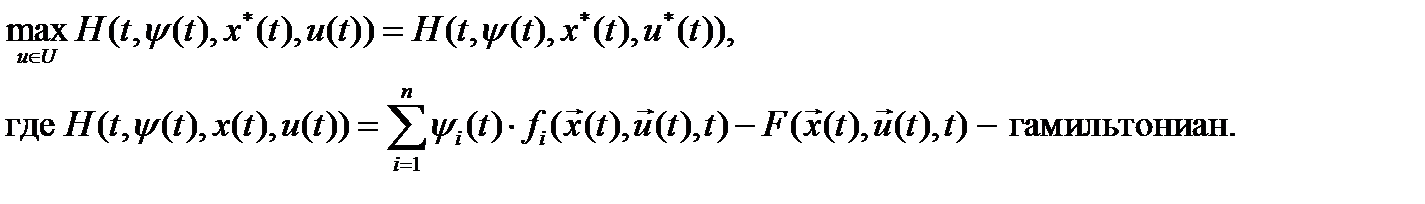
2). Функции 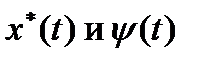 удовлетворяют системе канонических уравнений
удовлетворяют системе канонических уравнений
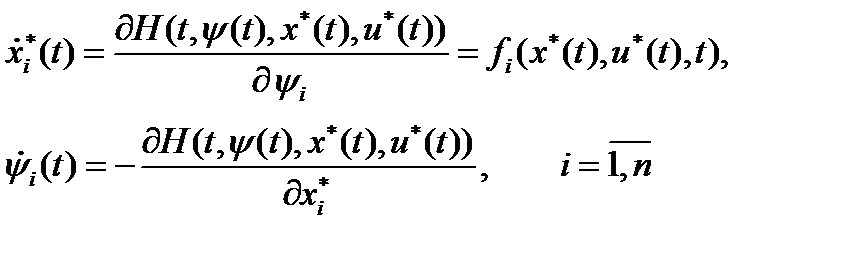
Функции  называются вспомогательными функциями.
называются вспомогательными функциями.
3). Выполняется условие трансверсальности
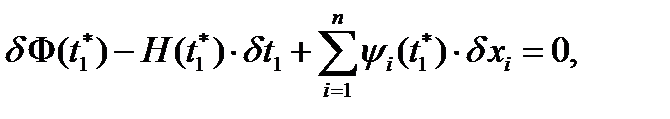
где вариации определяются следующим образом
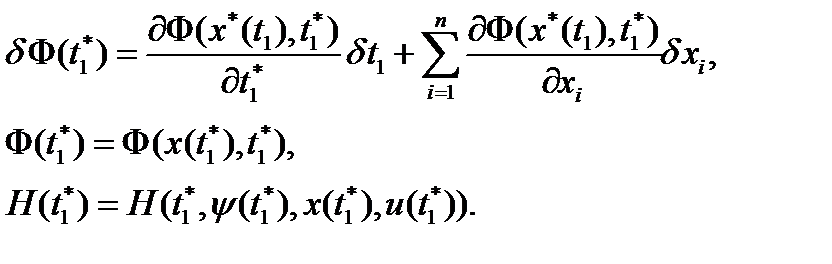
Если t 1 = const – задано, то 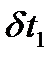 = 0, если t 1 не задано, то
= 0, если t 1 не задано, то 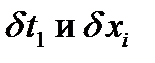 удовлетворяют системе уравнений
удовлетворяют системе уравнений
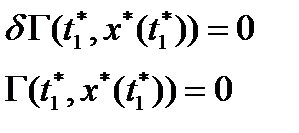
где 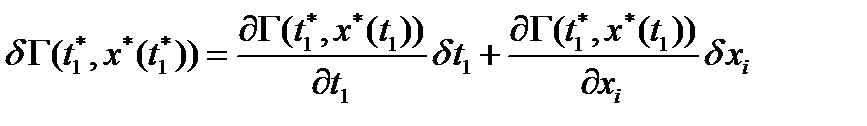 .
.
Здесь 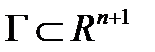 - некоторая гиперповерхность, достижением которой в момент времени t 1 определяется окончание процесса, если время окончания процесса t 1 не задано.
- некоторая гиперповерхность, достижением которой в момент времени t 1 определяется окончание процесса, если время окончания процесса t 1 не задано.
Алгоритм применения принципа максимума Понтрягина
1. Составить гамильтониан 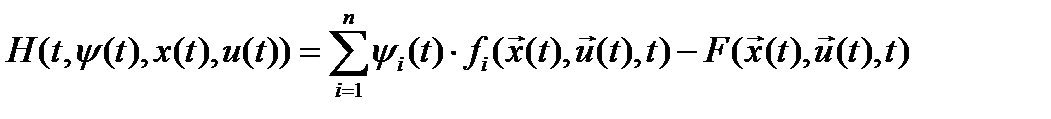 .
.
2. Найти структуру оптимального управления 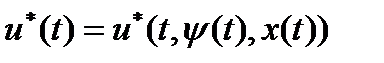 из условия максимума гамильтониана по управлению
из условия максимума гамильтониана по управлению 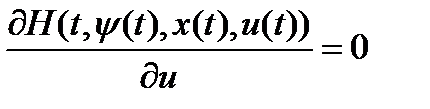 .
.
3. Составить систему канонических уравнений
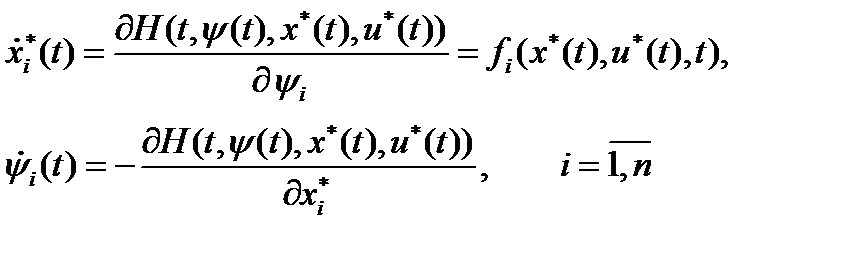
4. Получить недостающие краевые условия из условия трансверсальности
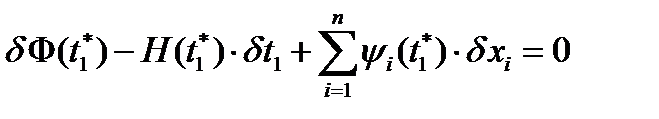 .
.
5. Решить двухточечную краевую задачу, полученную в п. 3, с учетом п. 2 и п. 4.
Пример.
Задача.
Даны модель объекта управления
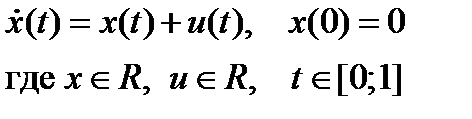
и функционал 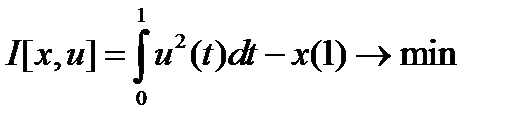 .
.
Требуется найти оптимальную траекторию 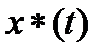 и оптимальное управление
и оптимальное управление 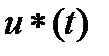 , на которых функционал достигает минимума.
, на которых функционал достигает минимума.
Функционал содержит интегральный и терминальный члены, следовательно, по классификации это задача Больца.
Определим функции, необходимые для составления гамильтониана:

Решаем задачу по алгоритму:
1. Составить гамильтониан 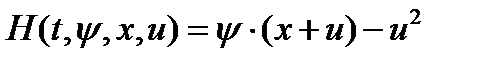
2. Найти структуру оптимального управления 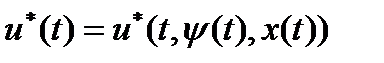 из условия максимума гамильтониана по управлению
из условия максимума гамильтониана по управлению 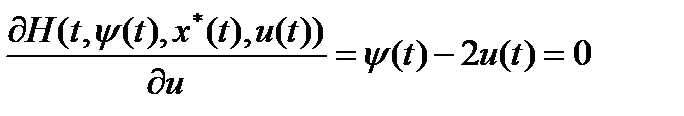 , откуда
, откуда 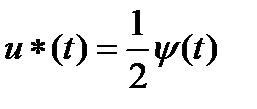 .
.
Равенство нулю первой производной является необходимым условием экстремума. Проверим, что в найденной точке гамильтониан достигает максимума, по знаку второй производной: 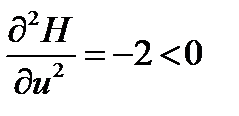 . Вторая производная отрицательная, следовательно, это точка максимума.
. Вторая производная отрицательная, следовательно, это точка максимума.
3. Составить систему канонических уравнений
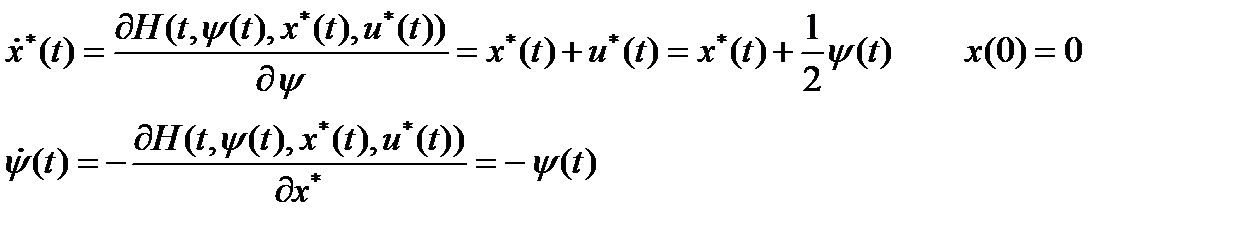
Мы получили систему двух дифференциальных уравнений с двумя неизвестными функциями 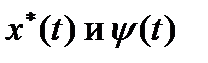 и только одним заданным граничным условием. Недостающее граничное условие найдем из условия трансверсальности.
и только одним заданным граничным условием. Недостающее граничное условие найдем из условия трансверсальности.
4. Получить недостающие краевые условия из условия трансверсальности, которое для случая, когда t 1= 1 задано, а число состояний (размерность вектора х) равно одному (n = 1), имеет вид 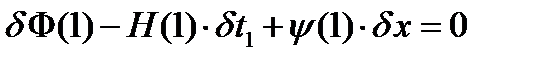 .
.
По условиям задачи:

Подставляя полученные результаты в уравнение трансверсальности, получаем уравнение
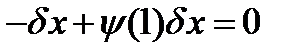 . Сокращаем полученное уравнение на
. Сокращаем полученное уравнение на 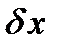 , после сокращения получаем
, после сокращения получаем 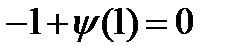 и в результате находим недостающее граничное условие
и в результате находим недостающее граничное условие 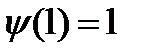 .
.
5. Решить двухточечную краевую задачу, полученную в п. 3, с учетом п. 2 и п. 4.
Решаем второе дифференциальное уравнение
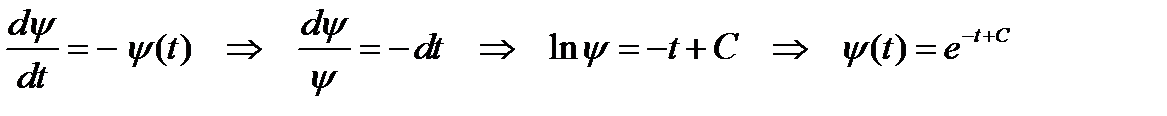
Постоянную интегрирования С находим из граничного условия 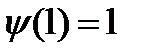 (п.4):
(п.4):
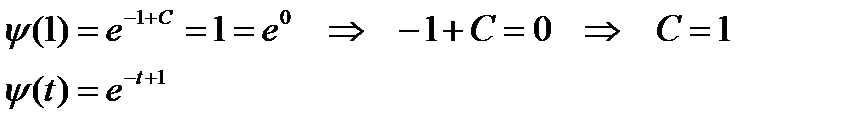
С учетом п.2 находим оптимальное управление 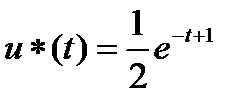
Подставляя полученный результат в первое каноническое уравнение, получаем
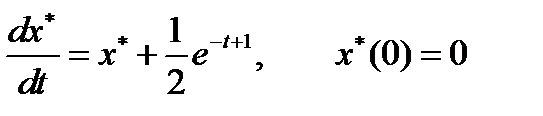 .
.
Полученное дифференциальное уравнение решаем в Matlab с помощью команды dsolve
>> syms x
>> dsolve('Dx=x+1/2*exp(1-t)','x(0)=0')
ans =
(exp(1)*exp(t))/4 - (exp(-t)*exp(1))/4
Оптимальная траектория описывается уравнением
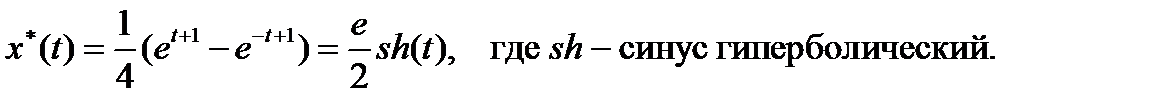
Ответ: оптимальная траектория 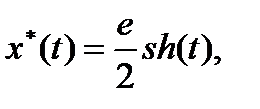 оптимальное управление
оптимальное управление 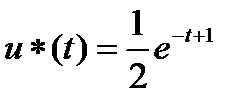 .
.
 2020-05-25
2020-05-25 716
716








