При исследовании сигналов часто используются методы спектрального анализа, позволяющие получить численные оценки частотного состава сигнала. Спектральный анализ основан на частотном подходе к анализу сигналов.
Наиболее распространены методики спектрального анализа, основанные на дискретном преобразовании Фурье (ДПФ):
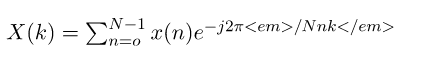
где х (n) — отсчеты дискретного сигнала, N — число отсчетов, а k = 0, 1, …, N – 1 — номера частотных составляющих разложения. Для ускорения расчета применяют алгоритмы быстрого преобразования Фурье (БПФ). В результате выполнения процедуры ДПФ получается ровно N значений комплексных чисел, описывающих гармонические колебания (синусоиды) с частотами 0, f 0, 2 f 0, 3 f 0…..(N – 1) f о, где f 0 = f Д/N-основная частота преобразования (f д частота дискретизации сигнала). Амплитуда и фазовый сдвиг каждой из синусоид определяются как модуль и аргумент соответствующего комплексного элемента разложения. По полученному разложению исходный сигнал может быть полностью восстановлен (в точках взятия отсчетов) с использованием процедуры обратного дискретного преобразования Фурье.
Па рис иллюстрируется процесс реконструкции фрагмента ЭКГ при помощи синусоид, определяемых значениями элементов ДПФ. Левые графики показывают синусоиды со значениями частот 0, f 0, 2 f 0, 3 f 0…..(N – 1) f о. а правые — этапы реконструкции сигнала с помощью этих синусоид. Рисунок позволяет проследить, как суммирование синусоидальных составляющих дает возможность получить описание кривой практически произвольной формы.

Рис. Иллюстрация процесса реконструкции фрагмента ЭКГ при помощи синусоид, определяемых значениями элементов ДПФ. В случае использования алгоритма БПФ для получения спектральных оценок возможны два основных варианта: расчет БПФ для всего фрагмента сигнала целиком (периодограммный метод) или использование усреднения спектров, рассчитанных по перекрывающимся фрагментам сигнала (метод Уэлча).
При использовании периодограммного метода выполняется следующая последовательность процедур:
· Удаление из сигнала среднего значения (или линейного тренда) с целью устранения постоянной составляющей.
· Умножение сигнала на сглаживающее окно (см. далее) для уменьшения спектральной утечки, вызываемой разрывами на краях анализируемого фрагмента, возникающими при его периодическом продолжении.
· Дополнение фрагмента сигнала нулями до размера, соответствующего какой-либо целой степени числа «2», что позволяет далее использовать алгоритм БПФ.
· Расчет дискретного преобразования Фурье с помощью алгоритма БПФ.
· Расчет спектральной плотности мощности (СПМ):
· 
· где f д частота дискретизации, f k = kl Δ f = k f д/N, k= 0, 1,2, … …,N/2, а X(f k) и p(f k) — соответственно значения компонентов разложения по Фурье и СПМ для частот f k.
· Умножение СПМ на корректирующий коэффициент, учитывающий потери мощности при использовании сглаживающего окна:

где Nw — размер окна в отсчетах, a w (n) — отсчеты оконной функции.
· Умножение СПМ на корректирующий коэффициент, учитывающий потерн мощности при дополнении нулями:
kо = N/No,
где No — число отсчетов фрагмента сигнала до дополнения нулями.
При использовании метода Уэлча исходный сигнал разбивается на сегменты, для каждого из которых спектральная оценка рассчитывается при помощи описанной выше процедуры. Далее полученные оценки усредняются по соответствующим частотам. Оценки спектральной плотности мощности, полученные с помощью метода Уэлча, отличаются большей статистической устойчивостью по сравнению с простым периодограммным методом.
Из-за того что при использовании ДПФ неявно предполагается бесконечное периодическое продолжение анализируемого сигнала, в получаемом спектре может наблюдаться эффект, называемый спектральной утечкой, который проявляется в «растекании» мощности спектральных составляющих по диапазону частот. Этот эффект может быть снижен за счет применения так называемых сглаживающих окон. Под последними понимаются функции, имеющие на краях близкие к нулю значения, которые плавно возрастают до единицы в средней части функции. На рис демонстрируется эффект спектральной утечки и результат ее снижения с использованием сглаживающего окна на левом верхнем графике показан фрагмент сигнала, представляющего собой смесь двух синусоид (с частотами 7 Гц и 13 Гц). Справа сверху показан амплитудный спектр этого сигнала, где для составляющей с частотой 7 Гц наблюдается спектральная утечка. На нижнем левом графике показаны сглаживающая функция и сигнал, полученный в результате умножения исходного сигнала на эту функцию. Как можно видеть, значения последней функции приближаются к нулевым на концах фрагмента. Правый нижний график содержит амплитудный спектр полученного сигнала, в котором эффект спектральной утечки существенно снижен. Однако следует иметь в виду, что применение сглаживающих окон, хоть и снижает спектральную утечку, но приводит в то же время к ухудшению спектрального разрешения, т. е. способности спектра к различению близких по частоте составляющих.
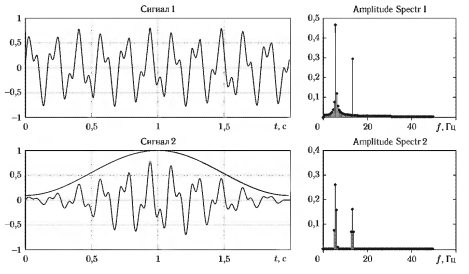
Снижение спектральной утечки при использовании сглаживающего окна
 2020-06-12
2020-06-12 456
456








