Необходимый признак возрастания (убывания) функции

Теорема 1. Если дифференцируемая функция y=f(x) возрастает (убывает) в данном интервале, то производная этой функции не отрицательна (не положительна) в этом интервале.

Обратное заключение также справедливо, оно выражается следующей теоремой.

Теорема 2. Если производная функции y=f(x) отрицательна (положительна) на некотором интервале, то функция в этом интервале монотонно возрастает (монотонно убывает).

Сформулируем теперь правило нахождения интервалов монотонности функции f(x).

1. Находим область определения функции f(x).

2. Вычисляем производную f’(x) данной функции.

3. Находим точки, в которых f’(x)=0 или не существует. Эти точки называются критическими для функции f(x).

4. Делим область определения функции этими точками на интервалы. Они являются интервалами монотонности.

5. Исследуем знак f’(x) на каждом интервале. Если f’(x)›0, то на этом интервале f(x) возрастает; если f’(x)‹0, то на таком интервале функция f(x) убывает.

Рассмотрим теперь нахождение промежутков возрастания/убывания на конкретном примере функции.

Пример №1. Найти промежутки монотонности функции y=2x³-3x²-36x+5.

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную: y’=6x²-6x-36.

3. Находим критические точки: y’=0.

x²-x-6=0

Д=1-4*(-6)*1=1+24=25

x₁=-2, x₂=3

4. Делим область определения на интервалы:

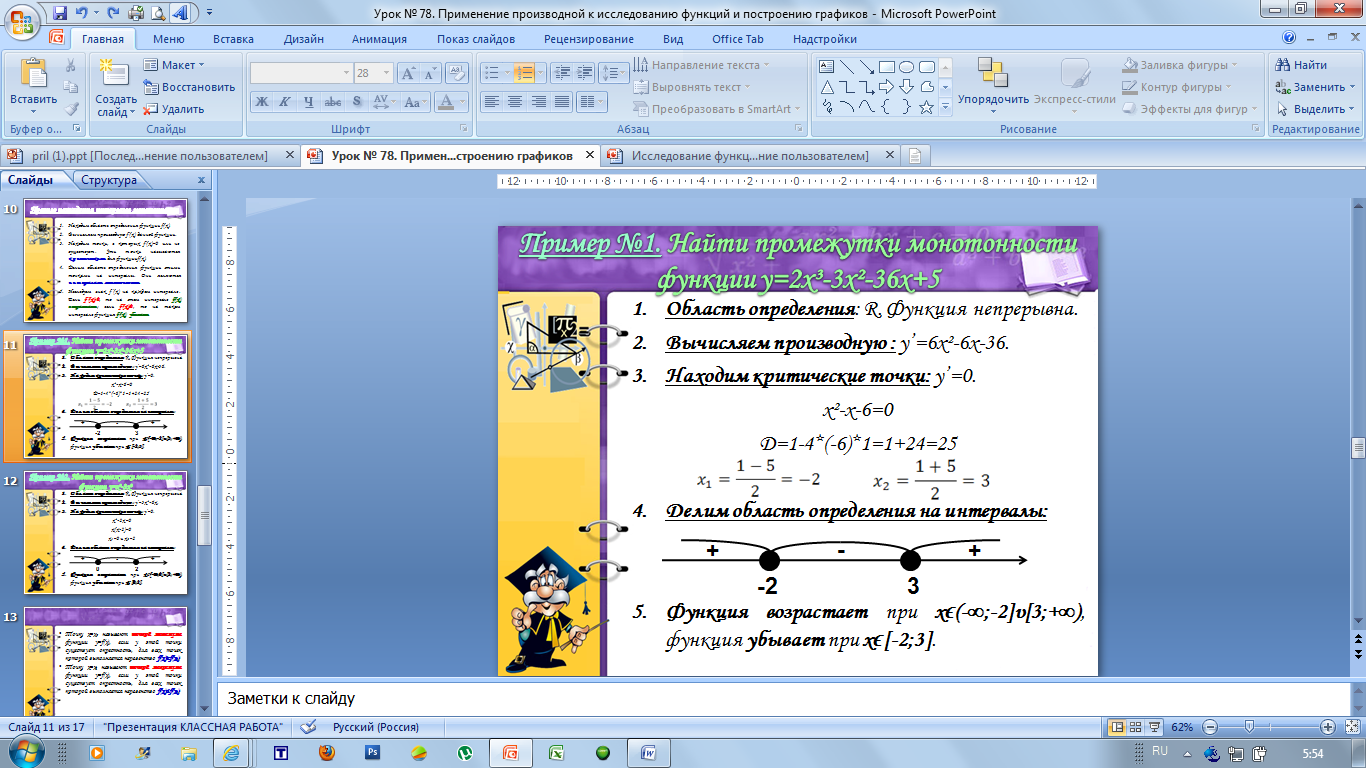
5. Функция возрастает при xϵ(-∞;-2]υ[3;+∞), функция убывает при xϵ[-2;3].

Пример №2. Найти промежутки монотонности функции y=x³-3x².

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную: y’=3x²-6x.

3. Находим критические точки: y’=0.

x²-2x=0

x(x-2)=0

x1=0 и x2=2

4. Делим область определения на интервалы:

5. Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].

Но помимо монотонности функций с помощью первой производной можно ещё определить экстремумы функций (точки максимума/минимума).

Сначала введём необходимые определения и понятия.

Опр. 1. Точку x=x₀ называют точкой минимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≥f(x₀).

Опр. 2. Точку x=x₀ называют точкой максимума функции y=f(x), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x)≤f(x₀).

Теорема 3. Если функция y=f(x) имеет экстремум в точке x=x₀, то в этой точке производная функции или равна нулю, или не существует.

Заметим, что теорема 3 является только необходимым (но не достаточным) условием существования экстремума: из того, что производная f’(x) в точке x0 обращается в нуль, не обязательно следует, что в этой точке функция имеет экстремум.

Например, функция f(x)=x⁵ имеет производную f’(x)=5x⁴, которая обращается в нуль в точке x₀=0. Однако экстремума в этой точке функция не имеет (происходит изменение кривизны).

Поэтому вводят ещё достаточный признак существования экстремумов функции.

Теорема 4. Если производная f’(x) при переходе через точку x₀ меняет знак, то точка x₀ является точкой экстремума функции f(x).

Если производная меняет знак с + на –, то точка будет являться точкой максимума, если с – на +, то точка будет точкой минимума.

Рассмотрим теперь на примерах исследование функции на монотонность и экстремумы.

Пример №3. Найти экстремумы функции y=-2x³-3x²+12x-4.

1. Область определения: R. Функция непрерывна.

2. Вычисляем производную: y’=-6x²-6x+12.

3. Находим критические точки: y’=0.

x²+x-2=0

D=1-4*1*(-2)=1+8=9

x₁=-2 и x₂=1

4. Делим область определения на интервалы:

5. Функция возрастает при xϵ(-∞;0]υ[2;+∞), функция убывает при xϵ[0;2].

6. Видно, что в точке x=-2 знак производной меняется с минуса на плюс. Поэтому критическая точка x=-2 – точка минимума. Найдём минимум функции y_min=-24. В точке x=1 знак меняется с плюса на минус. Поэтому критическая точка x=1 – точка максимума. Найдём максимум функции: y_max=3.