Этот вектор называется средним ускорением точки за время 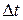 :
:

Предел, к которому стремится среднее ускорение при  , называется ускорением точки в данный момент времени:
, называется ускорением точки в данный момент времени:

Ускорение точки в данный момент времени равно векторной производной от скорости точки по времени.
Проекции ускорения точки на декартовые оси координат
Пусть положение точки определяется радиусом вектором  (рис. 2). Учитывая связь радиус-вектора с координатами точки
(рис. 2). Учитывая связь радиус-вектора с координатами точки  , подставляем это выражение в уравнение для скорости:
, подставляем это выражение в уравнение для скорости:
 .
.
При таком разложении вектора по координатным осям коэффициенты, стоящие при соответствующих орт-векторах, представляют собой проекции данного вектора на координатные оси, т.е.
 ,
,  ,
,  ,
, 
Таким образом, проекции скорости на координатные оси равны первым производным от соответствующих координат движущейся точки по времени. Эти производные находятся из уравнений движения точки.
Для определения модуля скорости получаем

Направление вектора  определяется его направляющими косинусами:
определяется его направляющими косинусами:
 ,
,  ,
, 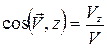 .
.
Для определения ускорения точки:
 ,
,
где  ,
,  ,
, 
Для определения модуля ускорения получаем

Направление вектора 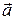 определяется его направляющими косинусами:
определяется его направляющими косинусами:
 ,
,  ,
,  .
.
 2020-06-08
2020-06-08 103
103








