2020-06-08
91
Криволинейное движение точки. Скорость, ускорение точки
Пусть движение задано в векторной форме 
. Точка 
движется по некоторой криволинейной траектории 
и ее положение определяется вектором 
. Пусть в момент времени 
положение точки 
определяется вектором 
. В момент времени 
, отличающейся от первоначального на бесконечно малый промежуток времени 
, точка занимает положение 
.
Таким образом, в каждый момент времени конец вектора 
будет находиться на траектории точки . Геометрическое место концов этих векторов, или линия, описываемая в пространстве концом вектора, начало которого находится в данной неподвижной точке, называется годографом этого вектора. Очевидно, что годографом радиуса-вектора 
движущейся точки является траектория 
этой точки. Соединим точки и 
прямой, тогда можно записать векторное равенство:
или 
,
где 
есть изменение (приращение) данного вектора за время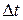 
.
рис. 7
Разделив это приращение на промежуток времени 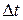, получим новый вектор, имеющий то же направление, но другую величину. Этот вектор 
называется средней скоростью точки за время :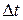
Средняя скорость криволинейного движения – это скорость такого равномерного движения, при котором точка, двигаясь по хорде равномерно, попадает на траекторию в то же положение, которое она занимает через данный промежуток времени, двигаясь по траектории неравномерно.
Будем теперь приближать 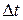к нулю. При этом точка 
будет приближаться к точке 
. В пределе направление вектора 
(так же, как и 
) совпадает с направлением касательной к траектории в точке , а модуль его равен 
. Предел средней скорости 
при 
называется скоростью движущейся точки в момент времени t:
Вектор скорости в данный момент времени равен векторной производной от радиуса вектора, определяющего положение точки, по времени. Вектор истинной скорости имеет направление касательной к траектории в данном положении точки.
Определим модуль вектора истинной скорости (без вывода).
…
,
где s=f(t).
