2020-06-08
200
(без вывода)
Касательное или тангенциальное ускорение:
Нормальное или центростремительное ускорение:
Оба вектора 
и 
лежат в соприкасающейся плоскости, значит, и итоговый вектор 
лежит в этой же плоскости, а проекция этого вектора на бинормаль равна нулю
Таким образом, проекция ускорения на направление скорости равна производной от модуля скорости по времени, а проекция ускорения на главную нормаль равна отношению квадрату скорости к радиусу кривизны траектории в той же точке, где в данный момент находится движущаяся точка.
Рассмотрим, как определяется ускорение точки для частных случаев движения.
1. Равномерное прямолинейное движение: 
, 
, 
,
, 
.
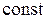2. Неравномерное прямолинейное движение: 
, , 
,
, 
, 
.
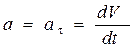3. Равномерное криволинейное движение: 
, 
, ,
, 
, 
.
4. Неравномерное криволинейное движение: 
, 
, ,
, 
, 
.
Используя связь между координатным и естественным способами задания движения точки, можно вывести зависимости, связывающие проекции ускорения на естественные и декартовые оси.
Практическое занятие Кинематика точки
Дано. Снаряд движется в вертикальной плоскости согласно уравнениям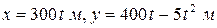 
. Определить траекторию движения снаряда, а также радиус кривизны траектории в начальной и наивысшей точках.
Решение. Получаем уравнение траектории из уравнений движения путем исключения параметра времени: 
– траектория парабола.
Далее
, 
, 
, 
.
Из полученных зависимостей следует, что все проекции, кроме 
, являются постоянными.
рис. 10
При
, 
, 
, 
, 
, 
, 
, 
.
Для определения радиуса кривизны в наивысшем положении рассмотрим снаряд в этом положении. Из рис. 10 видно, что в наивысшем положении скорость снаряда будет параллельна оси x, т.е. 
.
Тогда при 
, , 
, 
, ,
тогда
.
Ответ: , 
, 
.
