В этом случае траекторией движения точки является прямая линия. Положение точки определяется относительно начала отсчета (точки  ) координатой s. Чтобы определить положение точки
) координатой s. Чтобы определить положение точки  на траектории в любой момент времени, должна быть известна зависимость вида: s=f(t). Это уравнение характеризует закон движения точки вдоль оси s. Перемещение точки по траектории характеризуется скоростью ее движения, т.е. отношением пройденного пути к соответствующему промежутку времени.
на траектории в любой момент времени, должна быть известна зависимость вида: s=f(t). Это уравнение характеризует закон движения точки вдоль оси s. Перемещение точки по траектории характеризуется скоростью ее движения, т.е. отношением пройденного пути к соответствующему промежутку времени.

рис. 3
Рассмотрим два частных случая движения точки.
1. Равномерное движение, при котором отношение пройденного пути к соответствующему промежутку времени остается постоянным для любого промежутка времени: 
 ,
, 
 – скорость равномерного движения.
– скорость равномерного движения.

рис. 4
Пусть точка находится в начальный момент в положении 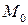 и движется вдоль оси s (рис. 4). Начало координат в точке
и движется вдоль оси s (рис. 4). Начало координат в точке  ; расстояние
; расстояние  . Тогда через промежуток времени
. Тогда через промежуток времени  точка будет находиться на расстоянии
точка будет находиться на расстоянии  или
или  . Получили закон равномерного движения точки:
. Получили закон равномерного движения точки:

2. Неравномерное прямолинейное движение – это движение, при котором скорость есть переменная величина, т.е. точка за равные промежутки времени проходит разные расстояния. Например,  .
.

рис. 5
Отношение пути s, пройденного точкой при неравномерном движении, ко времени  , в течение которого этот путь пройден, называется средней скоростью точки за данный промежуток времени
, в течение которого этот путь пройден, называется средней скоростью точки за данный промежуток времени  или на данном пути
или на данном пути  :
:

Средняя скорость характеризует быстроту движения за некоторый данный промежуток времени, но не дает представления о быстроте движения точки в отдельные моменты этого промежутка времени. Поэтому кроме средней скорости определяют мгновенную скорость точки в данный момент времени.
Скоростью точки в данный момент времени называется величина V, к которой стремится средняя скорость Vср при стремлении промежутка времени Dt к нулю:

Для прямолинейного движения этот вектор направлен вдоль траектории движения, и, учитывая, что производная может дать знак минус, вектор скорости может быть направлен как в сторону возрастания значения s, так и в сторону убывания значения s.
Ускорением точки в прямолинейном движении называется величина, характеризующая быстроту изменения скорости с течением времени, т.е. производная
 , тогда
, тогда

Если скорость и ускорение имеют одинаковые знаки, то движение ускоренное, т.е. с течением времени скорость возрастает, а если скорость и ускорение имеют разные знаки, то движение будет замедленным.
Из зависимости  следует, что ускорение обращается в ноль в те моменты, когда величина скорости достигает минимума или максимума.
следует, что ускорение обращается в ноль в те моменты, когда величина скорости достигает минимума или максимума.
Если преобразовать (изобразить) функциональную зависимость между s, V, a и временем t графически, то эти кривые называются соответственно графиками движения, скорости и ускорения (рис. 6).
Например, 

рис. 6
Рассмотрим частный случай. Если ускорение сохраняет свое значение за все время движения 
 , то такое движение называю равномерно-переменным.
, то такое движение называю равномерно-переменным.
Получим закон такого движения: 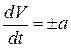 ,
,  ,
,  ,
,  или
или  .
.  ,
,  ,
,
 ,
,  .
.
Таким образом, зависимости для равномерно-переменного движения имеют вид

 ,
,  ,
, 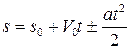 .
.
 2020-06-08
2020-06-08 108
108








